Czym się różni uczenie maszynowe od statystyki

Wbrew powszechnemu przekonaniu, uczenie maszynowe nie jest niczym nowym – tak naprawdę istnieje już od kilkudziesięciu lat. Początkowo było jednak odstawiane na bok, ze względu na duże wymagania obliczeniowe i ograniczenia mocy obliczeniowej sprzętu. Jednak w ostatnich latach, z powodu lawiny danych wynikającej z eksplozji informacyjnej i wzrostu mocy obliczeniowej komputerów, uczenie maszynowe zaczęło gwałtownie się rozwijać.

Ponieważ statystyka i uczenie maszynowe zajmują się podobnymi rzeczami (przetwarzaniem danych i wyciąganiem wniosków), niektórzy twierdzą, że to dziedziny tożsame. Dlaczego zatem nie kończymy wydziałów statystyki z dyplomami uczenia maszynowego? Właśnie dlatego, że – mimo wszelkich podobieństw – statystyka i uczenie maszynowe to dwie różne rzeczy.

Często słyszę wyjaśnienie w rodzaju: „Główną różnicą między maszynowym uczeniem a statystyką jest ich cel. Modele uczenia maszynowego są zaprojektowane tak, aby umożliwić jak najdokładniejsze przewidywania. Modele statystyczne są przeznaczone do wnioskowania o relacjach pomiędzy zmiennymi”. Technicznie to prawda, ale nie daje to szczególnie wyraźnej i satysfakcjonującej odpowiedzi.

ISTOTNĄ RÓŻNICĄ MIĘDZY UCZENIEM MASZYNOWYM a statystyką jest – rzeczywiście – ich cel. Jednak mówienie, że uczenie maszynowe to przede wszystkim dokładne przewidywania, podczas gdy modele statystyczne są przeznaczone do wnioskowania, jest stwierdzeniem niemal bezsensownym.

Po pierwsze, musimy zrozumieć, że istnieją statystyki i modele statystyczne. Statystyka jest matematycznym badaniem danych – nie można robić statystyk bez danych. Model statystyczny jest modelem dla danych, który jest używany (wykorzystuje dane) albo do wywnioskowania czegoś na temat relacji w obrębie danych, albo do stworzenia (innego, nowego) modelu zdolnego przewidzieć przyszłe wartości (często te dwa elementy idą w parze).

Są zatem dwa osobne zagadnienia, które powinniśmy omówić. Po pierwsze, czym różnią się statystyki od uczenia maszynowego. Po drugie, czym różnią się modele statystyczne od uczenia maszynowego.

Spróbujmy wyjaśnić to lepiej. Istnieje wiele modeli statystycznych, które mogą dokonywać przewidywań, ale dokładność nie jest ich mocną stroną. Modele uczenia maszynowego zapewniają natomiast różne stopnie interpretacji danych (od wysoce interpretowalnej regresji typu lasso po sieci neuronowe), ale generalnie poświęcają interpretacyjność na rzecz mocy predykcyjnej.

Są jednak przypadki, w których to wyjaśnienie nie pomoże nam zrozumieć różnic między uczeniem maszynowym a modelowaniem statystycznym. Spójrzmy na przykład regresji liniowej.

Wydawać by się mogło, że to właśnie podobieństwo metod stosowanych w modelowaniu statystycznym i uczeniu maszynowym spowodowało, że ludzie zakładają, że dziedziny te są tym samym. Jednak to nieprawda.

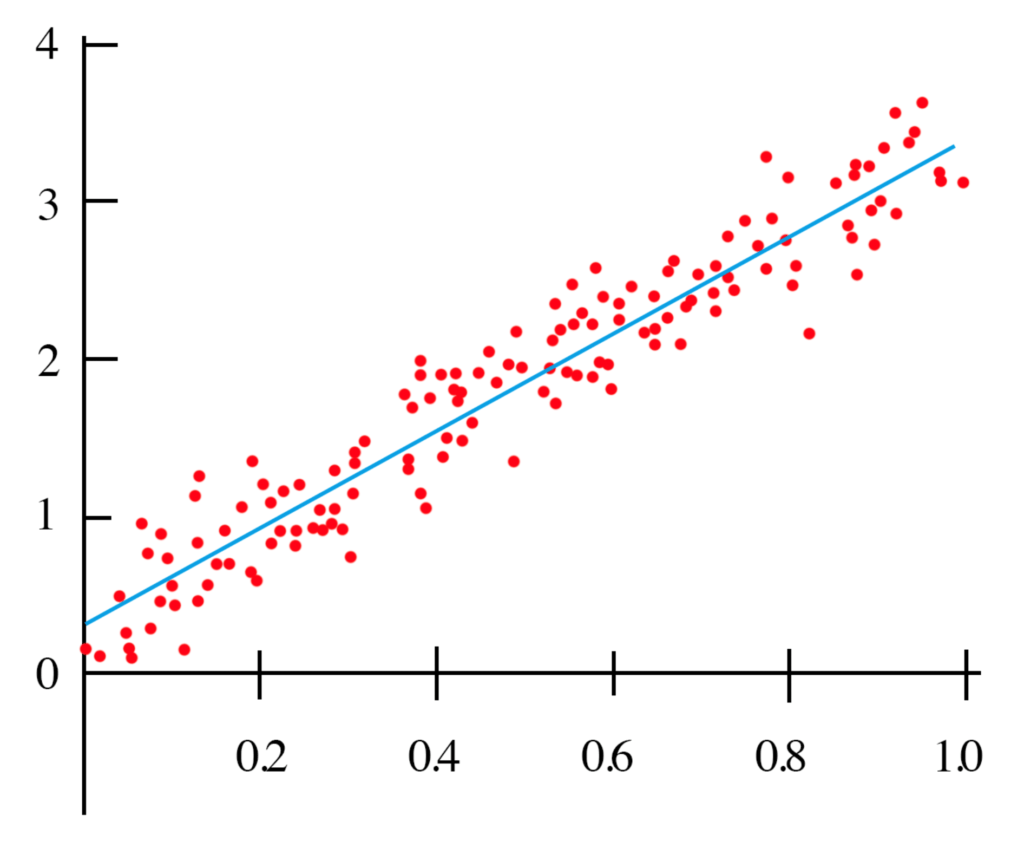
NAJBARDZIEJ OCZYWISTYM PRZYKŁADEM jest przypadek regresji liniowej, która jest prawdopodobnie główną przyczyną tego nieporozumienia. Regresja liniowa jest metodą statystyczną. Możemy trenować regresor liniowy i uzyskać taki sam rezultat, jak model regresji statystycznej, mający na celu zminimalizowanie kwadratowego błędu pomiędzy punktami danych.

Widzimy, że w jednym przypadku robimy coś, co nazywamy „treningiem” – czyli model, w którym wykorzystujemy podzbiór naszych danych. Nie wiemy, jak dobrze model będzie działał, dopóki nie przetestujemy tych danych na takich, które nie były obecne podczas szkolenia (zwanych zestawem testowym). Celem uczenia maszynowego w tym przypadku jest uzyskanie największej wydajności na zestawie testowym.

Dla modelu statystycznego znajdujemy linię (zob. wykres), która minimalizuje średni błąd kwadratowy na wszystkich danych, zakładając, że dane są liniowym regresorem z dodanym przypadkowym hałasem, który jest typowo gausowski z natury. Nie jest konieczny trening ani żaden zestaw testowy. W wielu przypadkach, szczególnie w badaniach (takich jak poniższy przykład czujnika), celem modelu jest scharakteryzowanie zależności pomiędzy danymi a zmienną wynikową, a nie przewidywanie przyszłych danych. Procedurę tę nazywamy wnioskowaniem statystycznym, w przeciwieństwie do przewidywań. Możemy jednak nadal używać tego modelu do przewidywania, a to może być głównym celem. Jednak sposób, w jaki model jest oceniany, nie będzie obejmował zestawu testów, a zamiast tego będzie obejmował ocenę znaczenia i solidności parametrów modelu.

CELEM (NIENADZOROWANEGO) UCZENIA MASZYNOWEGO jest uzyskanie modelu, który umożliwia powtarzalne przewidywania. Zazwyczaj nie obchodzi nas, czy model jest możliwy do zinterpretowania, chociaż zawsze polecam testowanie, aby zapewnić, że przewidywania modelu mają sens. Natomiast modelowanie statystyczne polega bardziej na znajdowaniu związków pomiędzy zmiennymi i znaczeniem tych związków, a jednocześnie na przewidywaniu.

Aby podać konkretny przykład różnicy między tymi dwiema procedurami, podam osobisty przykład. W ciągu dnia jestem naukowcem zajmującym się SI i pracuję głównie z danymi z czujników lub kamer. Jeśli próbuję udowodnić, że czujnik jest w stanie reagować na pewien rodzaj bodźców (takich jak np. zwolnienie miejsca na półce), użyłbym modelu statystycznego w celu ustalenia, czy odpowiedź na sygnał jest statystycznie istotna. Postarałbym się zrozumieć tę zależność i przetestować jej powtarzalność, aby móc dokładnie scharakteryzować odpowiedź czujnika i wyciągnąć wnioski w oparciu o te dane. Niektóre rzeczy mogą sprawdzić, czy odpowiedź jest w rzeczywistości liniowa, czy może być przypisana do rozmiaru przestrzeni, a nie jest przypadkowym hałasem w czujniku itp.

W przeciwieństwie do tego, mogę również uzyskać tablicę 20 różnych czujników i użyć jej, by spróbować przewidzieć reakcję mojego nowo scharakteryzowanego czujnika. Może się to wydawać nieco dziwne, jeśli nie wiemy zbyt wiele o czujnikach, ale jest to obecnie ważny obszar nauki. Model z 20 różnymi zmiennymi przewidującymi wynik mojego czujnika jest wyraźnie zorientowany na przewidywanie i nie spodziewam się, że będzie szczególnie możliwy do zinterpretowania. Ten model prawdopodobnie byłby czymś nieco bardziej enigmatycznym niż sieć neuronowa. Chciałbym, aby model miał sens, ale tak długo, jak potrafię trafnie przewidywać, byłbym całkiem zadowolony.

JEŚLI SPRÓBUJĘ UDOWODNIĆ ZWIĄZEK między moimi zmiennymi w stopniu istotności statystycznej, aby móc je opublikować w pracy naukowej, użyłbym modelu statystycznego, a nie uczenia maszynowego. Dzieje się tak dlatego, że bardziej zależy mi na relacji między zmiennymi niż na przewidywaniu. Dokonywanie przewidywań może być nadal ważne, ale brak możliwości interpretacji zapewnianej przez większość algorytmów uczenia maszynowego utrudnia udowodnienie zależności w obrębie danych (jest to obecnie duży problem w badaniach naukowych, gdzie badacze używają algorytmów, których nie rozumieją).

Powinno być jasne, że te dwa podejścia różnią się od siebie pod względem celu, pomimo zastosowania podobnych środków, aby się do tego celu dostać. Ocena algorytmu uczenia maszynowego wykorzystuje zestaw testowy do walidacji jego dokładności. Natomiast w przypadku modelu statystycznego, analiza parametrów regresji za pomocą przedziałów ufności, testów istotności i innych testów może być wykorzystana do oceny zasadności modelu. Ponieważ metody te dają ten sam wynik, łatwo jest zrozumieć, dlaczego można mylnie założyć, że są takie same.

Zanim przedyskutujemy, czym się różni statystyka i uczenie maszynowe, przedyskutujmy najpierw temat podobieństwa.

W rzeczywistości uczenie maszynowe (ML) opiera się na statystyce. Powinno to być oczywiste, ponieważ obejmuje dane, a dane muszą być opisane przy użyciu ram statystycznych. Uczenie maszynowe jest oparte również o wiele innych dziedzin spoza statystyki. Mowa między innymi o dziedzinach matematyki i informatyki, na przykład:

• Teoria ML z dziedzin takich jak matematyka i statystyka;
• Algorytmy ML z dziedzin takich jak optymalizacja, algebra macierzy, rachunek;
• Wdrożenia ML z zakresu informatyki i koncepcji inżynieryjnych.

GŁÓWNA RÓŻNICA MIĘDZY STATYSTYKĄ a uczeniem maszynowym polega na tym, że statystyka opiera się wyłącznie na przestrzeniach prawdopodobieństwa. Całość statystyk można zaczerpnąć z teorii zbiorów, która omawia, w jaki sposób możemy pogrupować liczby w kategorie zwane zbiorami, a następnie nałożyć miarę na ten zbiór, aby zapewnić, że łączna wartość wszystkich tych liczb wynosi 1. Nazywamy to przestrzenią prawdopodobieństwa. Statystyka nie zawiera żadnych innych założeń dotyczących wszechświata. Dlatego gdy określamy przestrzeń prawdopodobieństwa w bardzo rygorystycznych kategoriach matematycznych, określamy dokładnie 3 rzeczy.

Przestrzeń prawdopodobieństwa, którą tak określamy (Ω, F, P), składa się z trzech części:

1. Przykładowa przestrzeń (Ω), która jest zbiorem wszystkich możliwych wyników.
2. Zestaw zdarzeń (F), gdzie każde zdarzenie jest zestawem zawierającym zero lub więcej wyników.
3. Przypisanie prawdopodobieństw do zdarzeń (P), to jest funkcja od zdarzeń do prawdopodobieństw.

Uczenie maszynowe buduje się na statystycznej teorii, która opiera się na tym aksjomatycznym pojęciu przestrzeni prawdopodobieństwa. Teoria ta została opracowana w latach 60. i rozszerza się na tradycyjne statystyki. Istnieje kilka kategorii uczenia maszynowego. My skupimy się tylko na nadzorowanym podejściu, ponieważ jest to najłatwiejsze do wyjaśnienia.

Statystyczna teoria uczenia nadzorowanego mówi nam, że mamy zestaw danych, które określamy jako S = {(xᵢ,yᵢ)}. To w zasadzie oznacza tyle, że mamy zestaw n punktów danych, z których każdy jest opisany przez inne wartości, nazywanych przez nas cechami, i są one dostarczane przez x, a także te cechy są mapowane przez pewną funkcję, aby dać nam wartość y. Teoria ta mówi, że wiemy, że mamy te dane, a naszym celem jest znalezienie funkcji, która mapuje wartości x do wartości y. Taki zestaw wszystkich możliwych funkcji, które mogą opisywać to mapowanie, nazywamy przestrzenią hipotetyczną.

ABY ZNALEŹĆ TĘ FUNKCJĘ, MUSIMY dać algorytmowi jakiś sposób na „nauczenie się”, jaka jest najlepsza metoda podejścia do problemu. Jest to zapewnione przez coś, co nazywa się funkcją straty. Tak więc dla każdej hipotezy (proponowanej funkcji), którą mamy, musimy ocenić, jak funkcja ta działa, patrząc na wartość jej oczekiwanego ryzyka w odniesieniu do wszystkich danych. Oczekiwane ryzyko jest zasadniczo sumą funkcji straty pomnożoną przez rozkład prawdopodobieństwa danych. Gdybyśmy znali wspólny rozkład prawdopodobieństwa mapowania, łatwo byłoby znaleźć najlepszą funkcję. Tyle że to w ogóle nie jest znane, a zatem naszym zadaniem jest odgadnąć najlepszą funkcję, a następnie empirycznie zdecydować, czy funkcja straty jest lepsza, czy nie. Nazywamy to ryzykiem empirycznym.

Następnie możemy porównać kilka różnych funkcji i poszukać hipotezy, która daje nam minimalne oczekiwane ryzyko, czyli hipotezy dającej minimalną wartość (zwaną infimum) wszystkich hipotez na danych. Algorytm ma jednak tendencję do oszukiwania dla zminimalizowania jego funkcji strat poprzez nadmierne dopasowanie do danych. Dlatego po zapoznaniu się z funkcją opartą na danych zestawu treningowego funkcja ta jest zatwierdzana na zestawie testowym danych, które nie pojawiły się w zestawie treningowym. Charakter tego, jak właśnie zdefiniowaliśmy uczenie maszynowe, wprowadził problem nadmiaru dopasowania i uzasadnił potrzebę posiadania zestawu treningowo-testowego przy realizacji „uczenia”. Nie jest to nieodłączną cechą statystyk, ponieważ nie staramy się minimalizować ryzyka empirycznego.

ALGORYTM UCZENIA SIĘ, KTÓRY WYBIERA funkcję minimalizującą ryzyko empiryczne, nazywa się empiryczną minimalizacją ryzyka. Jako przykład weźmy prosty przypadek regresji liniowej. W tradycyjnym sensie staramy się zminimalizować błąd pomiędzy niektórymi danymi w celu znalezienia funkcji, która może być użyta do opisania danych. W tym przypadku, zazwyczaj używamy średniego kwadratowego błędu. Podnosimy go do kwadratu tak, aby dodatnie i ujemne błędy nie zniwelowały się nawzajem. Następnie możemy rozwiązać kwestię współczynników regresji w sposób zamknięty. Tak się składa, że jeśli weźmiemy naszą funkcję straty za średni kwadratowy błąd i wykonamy empiryczną minimalizację ryzyka, tak jak wymaga tego teoria statystycznego uczenia się, otrzymamy taki sam rezultat, jak tradycyjna analiza regresji liniowej. Dzieje się tak dlatego, że te dwa przypadki są równoważne w ten sam sposób, w jaki osiągnięcie maksymalnego prawdopodobieństwa na tych samych danych da nam ten sam rezultat. Maksymalne prawdopodobieństwo ma inny sposób osiągnięcia tego samego celu, ale nikt nie będzie się spierał i mówił, że maksymalne prawdopodobieństwo jest takie samo jak regresja liniowa.

Inną ważną kwestią, na którą należy zwrócić uwagę, jest to, że w tradycyjnych metodach statystycznych nie ma koncepcji szkolenia i zbioru testowego, ale używamy wskaźników, które pomogą nam zbadać, jak działa nasz model. Tak więc procedura oceny jest inna, ale obie metody są w stanie dać nam wyniki, które są solidne statystycznie. Kolejną sprawą jest to, że tradycyjne podejście statystyczne dało nam optymalne rozwiązanie, ponieważ rozwiązanie miało formę zamkniętą. Nie wypróbowano żadnych innych hipotez, ale zbliżono się do rozwiązania. Natomiast metoda uczenia maszynowego wypróbowała kilka różnych modeli, aby zbiec się z hipotezą końcową, która była zgodna z wynikiem zastosowania algorytmu regresji. Gdybyśmy użyli innej funkcji straty, wyniki nie byłyby zbieżne. Na przykład gdybyśmy użyli straty typu hinge loss, to wyniki nie byłyby takie same.

OSTATECZNEGO PORÓWNANIA MOŻNA DOKONAĆ, biorąc pod uwagę stronniczość modelu. Można by „poprosić” algorytm uczenia maszynowego o przetestowanie modeli liniowych, jak również modeli wielomianowych, modeli wykładniczych itd. Jest to równoznaczne ze zwiększeniem odpowiedniej przestrzeni na hipotezę. W tradycyjnym sensie statystycznym wybieramy jeden model i możemy ocenić jego dokładność, ale nie możemy automatycznie wybrać najlepszego modelu spośród 100 różnych modeli. Oczywiście w modelu zawsze występuje pewna stronniczość, która wynika z początkowego wyboru algorytmu. Jest to konieczne, ponieważ znalezienie arbitralnej funkcji, która jest optymalna dla zbioru danych, jest problemem trudnym do rozwiązania.

Więc co jest lepsze? To właściwie niemądre pytanie. Jeśli chodzi o statystykę i uczenie maszynowe, to uczenie maszynowe nie istniałoby bez statystyki. Ale uczenie maszynowe jest dość przydatne w dzisiejszych czasach ze względu na obfitość danych, do których ludzkość ma dostęp od czasu eksplozji informacji. Porównanie uczenia maszynowego i modeli statystycznych jest nieco trudniejsze. To, którego używamy, zależy w dużej mierze od tego, jaki jest cel. Jeśli po prostu pragniemy stworzyć algorytm, który będzie w stanie przewidzieć ceny mieszkań z dużą dokładnością lub użyć danych w celu określenia, uczenie maszynowe będzie prawdopodobnie lepszym podejściem. Jeśli próbujemy udowodnić związek między zmiennymi lub wyciągnąć wnioski z danych, to model statystyczny będzie prawdopodobnie lepszym podejściem. Niemniej, jeśli nie mamy silnego zaplecza w wiedzy o statystyce, nadal możemy studiować uczenie maszynowe i korzystać z niego. Wysoki poziom abstrakcji oferowany przez biblioteki programistyczne dla uczenia maszynowego sprawia, że całkiem łatwo jest ich używać nie będąc ekspertem w dziedzinie. Jednak nadal potrzebujemy minimalnego rozumienia podstawowych idei statystycznych, aby zapobiec nadmiarowi dopasowania modeli.

Skoro ustaliliśmy, że uczenie maszynowe (ML) jest dziedziną interdyscyplinarną, która wykorzystuje statystykę, omówmy niektóre z kluczowych pojęć szeroko stosowanych w ML.

PRAWDOPODOBIEŃSTWO I STATYSTYKA SĄ POWIĄZANYMI obszarami matematyki, które zajmują się analizą względnej częstotliwości zdarzeń. Prawdopodobieństwo dotyczy przewidywania przyszłych zdarzeń, natomiast statystyka obejmuje analizę częstotliwości zdarzeń z przeszłości.

Większość ludzi intuicyjnie rozumie stopniowanie prawdopodobieństwa, dlatego w naszej codziennej rozmowie używamy słów takich jak „prawdopodobnie” i „mało prawdopodobne”, ale będziemy rozmawiać o tym, jak wysuwać roszczenia ilościowe dotyczące tych stopni. W teorii prawdopodobieństwa zdarzenie jest zbiorem wyników eksperymentu, do którego przypisane jest prawdopodobieństwo. Jeśli E reprezentuje zdarzenie, to P(E) reprezentuje prawdopodobieństwo, że E wystąpi. Sytuacja, w której E może się zdarzyć (sukces) lub nie (porażka), nazywana jest próbą. To wydarzenie może być czymś w rodzaju rzucania monetą, rzucania kostką lub wyciągania kolorowej kuli z worka. W tych przykładach wynik zdarzenia jest losowy, więc zmienna reprezentująca wynik tych zdarzeń nazywana jest zmienną losową.

Rozważmy podstawowy przykład rzucania monetą. Jeśli moneta jest autentyczna, to wyrzucenie każdej ze stron jest tak samo prawdopodobne. Innymi słowy, gdybyśmy wielokrotnie rzucali monetą, spodziewalibyśmy się, że około połowa rzutów to awers, a połowa to rewers. W tym przypadku mówimy, że prawdopodobieństwo otrzymania awersu wynosi 1/2 lub 0,5.

PRAWDOPODOBIEŃSTWO EMPIRYCZNE OKREŚLA SIĘ na podstawie liczby powtórzeń zdarzenia podzielonej przez całkowitą liczbę zaobserwowanych incydentów. Jeśli dla n prób obserwujemy sukcesy s, prawdopodobieństwo sukcesu jest s/n. W powyższym przykładzie każda sekwencja rzutów monetami może mieć więcej lub mniej niż dokładnie 50 procent awersów.

Prawdopodobieństwo teoretyczne podaje się natomiast na podstawie liczby sposobów, na jakie dane zdarzenie może wystąpić, podzielonej przez całkowitą liczbę możliwych wyników. Tak więc awers może wystąpić raz, a możliwe wyniki to dwa (awers, rewers). Prawdziwe (teoretyczne) prawdopodobieństwo awersu wynosi 1/2.

Wspólne prawdopodobieństwo to prawdopodobieństwo wystąpienia zdarzeń A i B oznaczonych przez P(A i B) lub P(A ∩ B) jest prawdopodobieństwem wystąpienia zdarzeń A i B. Dotyczy to tylko sytuacji, gdy A i B są niezależne, co oznacza, że jeśli A wystąpiło, nie zmienia to prawdopodobieństwa B i odwrotnie.

Prawdopodobieństwo warunkowe jest również ważne.

Rozważmy, że A i B nie są niezależne, ponieważ jeśli A wystąpiło, prawdopodobieństwo B jest większe. Kiedy A i B nie są niezależne, często przydatne jest obliczenie prawdopodobieństwa warunkowego, P (A|B), które jest prawdopodobieństwem A danym, że B wystąpił: P(A|B) = P(A ∩ B)/ P(B).

Prawdopodobieństwo zdarzenia A uwarunkowanego zdarzeniem B jest oznaczone i zdefiniowane P(A|B) = P(A∩B)/P(B).

Podobnie, P(B|A) = P(A ∩ B)/P(A) . Możemy zapisać wspólne prawdopodobieństwo jako A i B jako P(A ∩ B)= P(A)P(B|A), co oznacza: „Szansa na obie rzeczy, które się wydarzyły, to szansa, że pierwsza z nich wydarzyła się, a potem druga podana pierwsza”.

TWIERDZENIE BAYESA TO ZWIĄZEK pomiędzy prawdopodobieństwem warunkowym dwóch zdarzeń. Na przykład jeśli chcemy znaleźć prawdopodobieństwo sprzedaży lodów w gorący i słoneczny dzień, twierdzenie Bayesa daje nam narzędzia do wykorzystania wcześniejszej wiedzy na temat prawdopodobieństwa sprzedaży lodów w każdy inny dzień (deszczowy, wietrzny, śnieżny itp.).

$$𝑃_{(𝐻|𝐸)} = { { 𝑃_{(𝐻)} \ast 𝑃_{(𝐸|𝐻)} } \over { 𝑃_{(𝐸)} } }$$

gdzie H i E są zdarzeniami, P(H|E) jest warunkowym prawdopodobieństwem wystąpienia zdarzenia H, biorąc pod uwagę, że zdarzenie E już wystąpiło. Prawdopodobieństwo P(H) w równaniu jest zasadniczo analizą częstotliwości; biorąc pod uwagę nasze wcześniejsze dane, jakie jest prawdopodobieństwo wystąpienia zdarzenia. P(E|H) w równaniu nazywa się prawdopodobieństwem i jest to zasadniczo prawdopodobieństwo, że dowody są poprawne, biorąc pod uwagę informacje z analizy częstotliwości. P(E) jest prawdopodobieństwem, że rzeczywiste dowody są prawdziwe.

Niech H reprezentuje zdarzenie, że sprzedajemy lody, a E jest zdarzeniem pogodowym. Wtedy możemy zapytać, jakie jest prawdopodobieństwo sprzedaży lodów w danym dniu, biorąc pod uwagę warunki atmosferyczne. Matematycznie jest to napisane tak: P(H = sprzedaż lodów | E = typ pogody), co odpowiada lewej stronie równania. P(H) po prawej stronie jest wyrażeniem znanym jako wcześniejsze, ponieważ możemy już znać marginalne prawdopodobieństwo sprzedaży lodów. W naszym przykładzie jest to P(H = sprzedaż lodów), tzn. prawdopodobieństwo sprzedaży lodów bez względu na rodzaj pogody na zewnątrz. Na przykład mógłbym spojrzeć na dane, które mówią, że 30 osób z potencjalnych 100 kupiło lody w jakimś sklepie. Więc mój P(H = sprzedaż lodów) = 30/100 = 0,3, zanim dowiedziałem się czegoś o pogodzie. W ten sposób twierdzenie Bayesa pozwala nam uwzględnić wcześniejsze informacje.

KLASYCZNYM ZASTOSOWANIEM TWIERDZENIA Bayesa jest interpretacja badań klinicznych. Załóżmy, że podczas rutynowego badania lekarskiego lekarz poinformuje nas, że wynik testu na rzadką chorobę jest pozytywny. Jesteśmy również świadomi, że wyniki tych badań nie muszą być pewne. Zakładając, że mamy czułość (zwaną również prawdziwie pozytywnym wskaźnikiem) dla 95 procent pacjentów z chorobą oraz swoistość (zwaną również prawdziwie negatywnym wskaźnikiem) dla 95 procent zdrowych pacjentów. Jeśli pozwolimy, aby wartości „+” i „-” oznaczały odpowiednio pozytywny i negatywny wynik testu, wówczas dokładność testu jest prawdopodobieństwem warunkowym: P(+|choroba) = 0,95, P(-|zdrowe) = 0,95. W kategoriach bayesowskich chcemy obliczyć prawdopodobieństwo wystąpienia choroby w teście pozytywnym, P(choroba|+).

$$𝑃_{(𝑐ℎ𝑜𝑟𝑜𝑏𝑎|+)} = { 𝑃_{(+|𝑐ℎ𝑜𝑟𝑜𝑏𝑎)} \ast 𝑃_{(𝑐ℎ𝑜𝑟𝑜𝑏𝑎)} \over 𝑃_{(+)} }$$

Jak ocenić P(+), czyli wszystkie pozytywne przypadki? Musimy rozważyć dwie możliwości, P(+|choroba) i P(+|zdrowe). Prawdopodobieństwo fałszywie pozytywnego wyniku, P(+|zdrowe), jest dopełnieniem P(-|zdrowe). Zatem P(+|zdrowe) = 0,05.

$$𝑃_{(𝑐ℎ𝑜𝑟𝑜𝑏𝑎|+)} = { 𝑃_{(+|𝑐ℎ𝑜𝑟𝑜𝑏𝑎)} 𝑃_{(𝑐ℎ𝑜𝑟𝑜𝑏𝑎)} \over {𝑃_{(+|𝑐ℎ𝑜𝑟𝑜𝑏𝑎)}𝑃_{(𝑐ℎ𝑜𝑟𝑜𝑏𝑎)} + 𝑃_{(+|𝑧𝑑𝑟𝑜𝑤𝑦)}𝑃_{(𝑧𝑑𝑟𝑜𝑤𝑦)}} }$$

Co ważne, twierdzenie Bayesa ujawnia, że w celu obliczenia warunkowego prawdopodobieństwa – iż mamy chorobę, której wynik testu był pozytywny, musisz znać „wcześniejsze” prawdopodobieństwo, że mamy chorobę P(choroba), biorąc pod uwagę brak jakichkolwiek informacji. Oznacza to, że musimy znać ogólną częstość występowania choroby w populacji, do której należymy. Zakładając, że testy te są stosowane w populacji, w której rzeczywista choroba wynosi 0,5%, P(choroba)= 0,005, co oznacza, że P(zdrowy) = 0,995.

Zatem:

$$𝑃_{(𝑐ℎ𝑜𝑟𝑜𝑏𝑎|+)} = { 0,95 \ast { 0,005} \over { 0,95 \ast 0,005 + 0,05 \ast 0,995 } } = { 0,088}$$

INNYMI SŁOWY, MIMO POZORNEJ WIARYGODNOŚCI testu, prawdopodobieństwo, że rzeczywiście jesteśmy chorzy, jest wciąż mniejsze niż 9 procent. Uzyskanie pozytywnego wyniku zwiększa prawdopodobieństwo wystąpienia choroby. Ale błędem jest interpretowanie dokładności testu na poziomie 95 procent jako prawdopodobieństwa wystąpienia choroby.

Statystyki opisowe odnoszą się do metod podsumowywania i porządkowania informacji w zbiorze danych. Wykorzystamy poniższą tabelę do opisania niektórych pojęć statystycznych.

nr	Stan cywilny	Hipoteka	Przychód	Ranga	Rok	Ryzyko
1	Singiel	Tak	146,709 zł	2	2009	Niskie
2	Żonaty	Tak	123,544 zł	7	2010	Niskie
3	Inne	Nie	96,519 zł	9	2011	Niskie
4	Inne	Nie	138,988 zł	3	2009	Niskie
5	Inne	Tak	127,405 zł	4	2010	Niskie
6	Inne	Nie	92,658 zł	10	2008	Wysokie
7	Żonaty	Tak	96,905 zł	8	2010	Niskie
8	Żonaty	Tak	185,317 zł	1	2007	Niskie
9	Żonaty	Tak	123,931 zł	6	2009	Wysokie
10	Żonaty	Tak	124,317 zł	5	2010	Niskie

Elementy: Podmioty, dla których gromadzone są informacje, nazywane są elementami. W powyższej tabeli elementami jest 10 wnioskodawców. Elementy nazywane są również przypadkami lub tematami.

Zmienne: Cecha elementu nazywana jest zmienną. Może przyjmować różne wartości dla różnych elementów, np. stanu cywilnego, hipoteki, dochodów, rangi, roku i ryzyka. Zmienne są również nazywane atrybutami.

Zmienne mogą mieć charakter jakościowy lub ilościowy.

Jakościowe: Zmienna jakościowa umożliwia klasyfikację elementów lub ich klasyfikację według pewnych cech. Zmienne jakościowe to stan cywilny, hipoteka, ranga i ryzyko. Zmienne jakościowe nazywane są również zmiennymi kategorycznymi.

Ilościowe: Zmienna ilościowa przyjmuje wartości liczbowe i umożliwia przeprowadzenie na niej znaczącej arytmetyki. Zmienne ilościowe to dochód i rok. Zmienne ilościowe nazywane są również zmiennymi numerycznymi.

Zmienna dyskretna: Zmienna numeryczna, która może przyjmować skończoną lub możliwą do policzenia liczbę wartości, jest zmienną dyskretną, dla której każda wartość może być odczytana jako oddzielny punkt, z odstępem między poszczególnymi punktami. Rok jest przykładem zmiennej dyskretnej.

Zmienna ciągła: Zmienna numeryczna, która może przyjmować nieskończenie wiele wartości, jest zmienną ciągłą, której możliwe wartości tworzą przedział na linii numerycznej, bez odstępu między punktami. Dochód jest przykładem zmiennej ciągłej.

Populacja: Populacja jest zbiorem wszystkich elementów interesujących dla danego problemu. Parametr jest cechą charakterystyczną populacji.

Próba: Próba składa się z podzbioru populacji. Charakterystyka próby nazywana jest statystyką.

Próba losowa: Kiedy pobieramy próbkę, dla której każdy element ma równe szanse na wybór.

MIARY „ŚRODKA”, JAK ŚREDNIA CZY MEDIANA, wskazują, gdzie w danych numerycznym znajduje się centralna część danych.

Średnia jest średnią arytmetyczną zbioru danych. Średnia z próby jest średnią arytmetyczną próbki i jest oznaczona jako x̄ („x-bar”). Średnia populacji jest średnią arytmetyczną populacji i jest oznaczona jako 𝜇 („myu”, grecka litera dla m).

Mediana jest środkową wartością danych, gdy jest nieparzysta liczba wartości danych i dane zostały posortowane w kolejności rosnącej. Jeżeli jest liczba parzysta, mediana jest średnią dwóch środkowych wartości danych.

Moda jest wartością danych, która występuje z największą częstotliwością. Zarówno zmienne ilościowe, jak i kategoryczne mogą mieć modę, ale tylko zmienne ilościowe mogą mieć średnie czy mediany. Każda wartość dochodu występuje tylko raz, więc nie ma mody. Modą na rok 2010 jest rok 2010, z częstotliwością 4.

Średni zakres jest średnią wartości maksymalnych i minimalnych w zbiorze danych.

Miary zmienności: Na przykład zakres, zmienność czy odchylenie standardowe. Pozwalają one określić ilość zmian lub rozproszenia występujących w danych.

Zakres zmiennej jest równy różnicy między wartością maksymalną i minimalną. Zakres dochodu jest równy:

$$𝑧𝑎𝑘𝑟𝑒𝑠 (𝑑𝑜𝑐ℎó𝑑) = { 𝑚𝑎𝑘𝑠𝑦𝑚𝑎𝑙𝑛𝑦 (𝑑𝑜𝑐ℎó𝑑) − 𝑚𝑖𝑛 (𝑑𝑜𝑐ℎó𝑑) } = { 185,317 – 92,658 = 92,659}$$

ZAKRES ODZWIERCIEDLA JEDYNIE RÓŻNICĘ pomiędzy największą i najmniejszą obserwacją, ale nie odzwierciedla tego, jak dane są scentralizowane.

Wariancja w populacji definiowana jest jako średnia kwadratowych różnic od średniej, oznaczonych jako 𝜎² („sigma-squared”):

$$\sigma^{2} = { { \sum {( x – \mu )^{2}} } \over { N } }$$

Większa wariancja oznacza, że dane są bardziej rozproszone.

Odchylenie próbki s² jest w przybliżeniu średnią kwadratowych odchyleń, przy czym N zastępuje się przez n-1. Różnica ta występuje, ponieważ średnia z próby jest używana jako przybliżenie średniej rzeczywistej populacji.

$$s^{2} = { { \sum{ (x – \bar{ x} )^{2} } } \over { n – 1 } }$$

Miary położenia to np. percentyl, wartość Z, kwartyle, mają za zadanie wskazanie względnego położenia określonej wartości danych w dystrybucji danych.

Percentyl zbioru danych jest wartością danych w taki sposób, że p procent wartości w zbiorze danych jest na poziomie x lub poniżej tej wartości. Pięćdziesiąty percentyl jest medianą.

Zasięg percentyla wartości danych równa się procentowi wartości w zbiorze danych, które są na poziomie lub poniżej tej wartości.

Wartość Z dla danej wartości danych przedstawia, ile odchyleń standardowych wartości danych znajduje się powyżej lub poniżej średniej.

$${𝑍 − 𝑠𝑐𝑜𝑟𝑒}={{(x-\bar{x})}\over{s}}$$

Tak więc, jeśli z jest dodatnie, oznacza to, że wartość jest powyżej średniej.

WYKRESY PUNKTOWE TO NAJPROSTSZY SPOSÓB wizualizacji zależności pomiędzy dwiema zmiennymi ilościowymi, x i y. Dla dwóch zmiennych ciągłych, wykres rozproszenia jest wspólnym wykresem. Każdy punkt (x, y) jest grafowany na płaszczyźnie kartezjańskiej, z osią x w poziomie i osią y w pionie. Wykresy rozproszenia są czasami nazywane wykresami korelacyjnymi, ponieważ pokazują, w jaki sposób skorelowane są dwie zmienne.

Korelacja jest statystyką mającą na celu ilościowe określenie siły relacji między dwiema zmiennymi. Współczynnik korelacji r określa siłę i kierunek zależności liniowej pomiędzy dwiema zmiennymi ilościowymi. Współczynnik korelacji jest definiowany jako:

$$r={{\sum{(x-\bar{x})(y-\bar{y})}}\over{(n-1)s_{x}s_{y}}}$$

gdzie s_x i s_y reprezentują odchylenie standardowe odpowiednio zmiennej x i zmiennej y. −1 ≤ r ≤ 1.

Jeśli r jest dodatnie i znaczące, mówimy, że x i y są dodatnio skorelowane. Wzrost wartości x jest związany ze wzrostem wartości y.

Jeśli r jest ujemne i znaczące, mówimy, że x i y są negatywnie skorelowane. Wzrost wartości x jest związany ze spadkiem wartości y.

Podsumowując, opisane powyżej podstawowe pojęcia prawdopodobieństwa i statystyki są obowiązkowe dla każdego, kto jest zainteresowany uczeniem maszynowym, nawet korzystając z wysokopoziomowych bibliotek programistycznych. Pokrótce omówione zostały niektóre z podstawowych pojęć, które są najczęściej używane w uczeniu maszynowym.

Mam nadzieję, że nauczyłeś się czegoś nowego i użytecznego. Czegoś, co zaprocentuje w Twoich projektach.

• edukacja
• nauka
• prawdopodobieństwo
• sieci neuronowe
• statystyka
• uczenie maszynowe / machine learning