Wagi wyjaśnialiśmy na przykładzie zakupu warzyw. Mogliśmy tych warzyw wziąć więcej lub mniej. W tym przykładzie chcieliśmy pokazać, że końcowy wynik może być różny, a wszystko zależy właśnie od wagi. Oczywiście w sztucznych neuronach nie chodzi o wagę w rozumieniu: ile coś waży, tylko o to, czy jest lub nie jest dla nas ważne. Spróbujemy wyjaśnić to na prostym przykładzie:

Jak nauczyć sztuczną inteligencję odróżniać na obrazie koło od kwadratu?

Jeśli czytałeś poprzedni artykuł, to wiesz, że SI, kiedy patrzy na obraz, by się nauczyć, co na nim widzi, analizuje każdy jego najmniejszy fragment. Taki najmniejszy fragment to piksel. Tak więc pokażemy naszej sztucznej inteligencji obraz koła. Z racji tego, że bada ona każdy piksel, rozrysowaliśmy to koło właśnie w postaci pikseli:

Wejścia: Aby sztuczna inteligencja mogła „zobaczyć” obraz i nauczyć się, że jest na nim koło, neuron, który będzie badał obraz, ma 36 wejść. Jedno wejście = zbadanie jednego piksela. Każdy piksel ma wartość 1.

Wagi: Wiesz już, że sygnał odebrany przez wejście trafia do wagi, czyli zostanie przez nią pomnożony.

Dlatego ustalimy dwie wagi:
jasny piksel = 0
żółty piksel = 1

Teraz nałożymy wagi na wejścia:

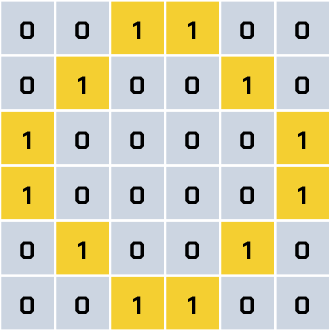
Wiemy, że w bloku sumującym neuronu wykonywane są obliczenia według wzoru:
ewentualna stała + waga1 × wejście1 + waga2 × wejście2 +… = wynik (gdzie w miejsce … wstawiamy iloczyny kolejnych wag i wejść).

Moglibyśmy rozpisać to bardzo szczegółowo rzędami, np. pierwszy rząd:
0 × 1 + 0 × 1 + 1 × 1 + 1 × 1 + 0 × 1 + 0 × 1 = 0 + 0 + 1 + 1 + 0 + 0 = 2

Jednak to nie ma sensu i byłoby czasochłonne. Możemy obliczyć to szybciej. Skoro wiemy, że mamy na obrazie 12 wag o wartości 1, to 12 × 1 = 12. Wszystkie piksele bez koloru dają wartość 0 (24 × 0 = 0), zatem neuron zwróci nam wartość 12. Czy w ten sposób sztuczna inteligencja rozpozna koło? Jeszcze nie odpowiemy na to pytanie, ale pójdziemy o krok dalej…

Teraz pokażemy sztucznej inteligencji obraz kwadratu. Wagi już nałożyliśmy na wejścia, zgodnie z tą samą zasadą, którą zastosowaliśmy przy obrazie koła.

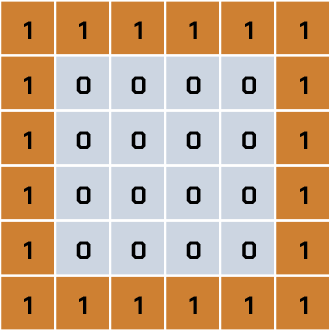
Neuron w przypadku kwadratu zwróci nam wartość 20, bo mamy 20 wag o wartości 1, a pozostałe mają wartość 0. Możesz to policzyć i sprawdzić, jeśli masz ochotę.

Teraz porównajmy nasze koło i kwadrat w liczbach.
Koło = 12, kwadrat = 20. Jak te figury na podstawie liczb rozróżni sztuczna inteligencja? Otóż… nie odróżni. W odróżnieniu koła od kwadratu pomoże sztucznej inteligencji funkcja progowa, która działa na zasadzie warunku: jeśli wynik jest większy od 0, to na obrazie jest kółko; jeśli jest mniejszy od 0, to na obrazie jest kwadrat.

Zatem w przypadku kwadratu musimy ustawić inne wagi, np. -1. Jeśli to zrobimy, to teoretycznie wynik zwrócony przez sztuczny neuron powinien wynieść -20. Wtedy funkcja progowa zadziałałaby zgodnie z warunkiem. Dość dużo tych obliczeń, prawda? A co by było, gdyby obraz miał 1000 na 1000 pikseli? Spróbujemy uprościć sprawę wag. Nałożymy więc na siebie obrazy koła i kwadratu:

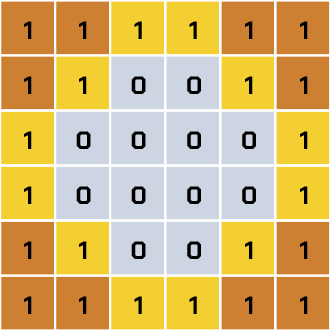
Zastanawiasz się, w czym problem? To spójrz na następny obraz, na którym piksele wspólne dla koła i dla kwadratu zaznaczyliśmy na ciemnobrązowo:

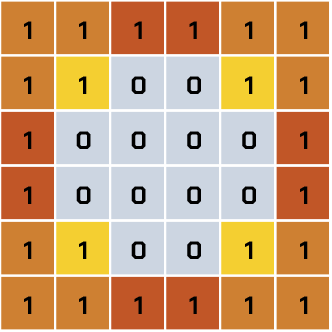
Problem tkwi w ciemnobrązowych pikselach. Skoro są takie same dla koła i kwadratu, to przyznasz, że szanse na to, by na ich podstawie sztuczna inteligencja rozróżniała te dwie figury, są znikome. Nasuwa się więc wniosek, że nie ma potrzeby ustalania dla nich wag. Pojawia się też pytanie: dla których wejść warto wagi ustalać?

Odpowiedź: dla warstw charakterystycznych dla danej figury. Warstwy charakterystyczne to takie, które pojawią się właśnie przy konkretnej figurze, a dla innej pozostają puste. Zwróć uwagę, że koło nigdy nie zapełni rogów obrazu, a kwadrat – na pewno.

Popatrzmy więc jeszcze raz na obie figury i zastanówmy się, gdzie warto ustawić wagi:

Oto proponowane rozwiązanie:

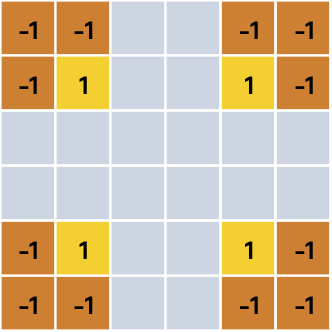
Czy jest jeszcze prostsze rozwiązanie? Oczywiście. Nie musimy ustalać wag dla każdego rogu obrazka. Moglibyśmy dla jednego w ten właśnie sposób:

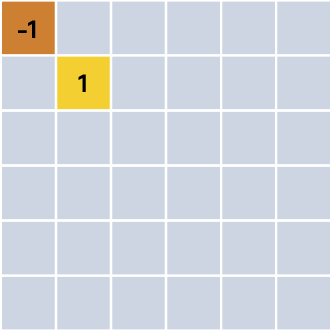
Gdy SI „zobaczy” kwadrat, wynik z bloku sumującego będzie równy -1, a gdy koło, wynik wyniesie 1. Wynik zostanie przesłany do bloku funkcji. W takich sytuacjach funkcja progowa „wybiera” zgodnie z warunkiem: Jeśli wynik jest mniejszy od 0, na obrazie jest kwadrat. Jeśli jest większy od 0, na obrazie jest koło. Wszystko się zgadza.

Pamiętaj, że omówiony przykład rozróżniania koła i kwadratu sprawdzi się tylko wtedy, gdy pokazujemy sztucznej inteligencji te dwa obrazy i zawsze są one takich samych rozmiarów. Jeśli zastanawiasz się, dlaczego, to podpowie Ci poniższy obrazek:

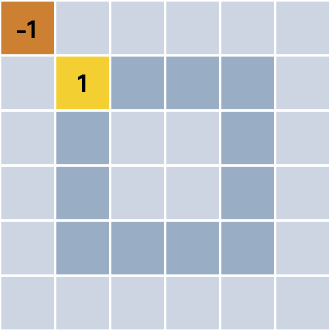
To były bardzo proste przykłady ustalania wag.
Zadanie oczywiście jest o wiele trudniejsze, gdy mamy do czynienia z figurami różnej wielkości na tym samym obrazie. Jeszcze większe trudności sprawia sztucznej inteligencji obejrzenie obrazu, który ma ogromny rozmiar. Obraz wielkości 1000 na 1000 pikseli wymagałby od neuronu… miliona wejść, żeby zbadać, piksel po pikselu, co na nim jest. W takich sytuacjach stosuje się tzw. splotowe sieci neuronowe (inaczej: konwolucyjne). Neurony w warstwie wejściowej mają o wiele mniej wejść i oglądają obraz kawałek po kawałku. Wykrywają jasne i ciemne plamki oraz konkretne kolory. Rozpoznają krawędzie i kształty elementów, a nawet ich orientację, czyli to, że np. są obrócone o 90 stopni w prawo. Najważniejszą cechą sieci konwolucyjnych jest to, że potrafią rozpoznać wspomniane kółko czy kwadrat bez względu na to, czy będzie on zajmował cały obraz, czy jego ćwierć. Rozpoznają je nawet wtedy, gdy są przechylone, w innych pozycjach niż te, w których neurony „widziały” je podczas nauki.

Czas na sprawdzenie wiedzy. Pamiętaj, że możesz zawsze sprawdzić, czy dobrze odpowiedziałeś na poniższe pytania, stosując obliczenia: waga1 × wejście1 + waga2 × wejście2… = wynik.

Wynik powinien być mniejszy lub większy od zera, gdyż w poniższych zadaniach zastosowaliśmy funkcję progową.