Wszystkie otaczające nas obrazy, dźwięki, zapachy, smaki, a nawet ból czy łaskotanie odbieramy dzięki neuronom.
Neuron, czyli komórka nerwowa, to najmniejszy element układu nerwowego. Rejestruje bodziec, na przykład ukłucie szpilką, i przekazuje go następnemu neuronowi. Przekazywanie bodźca przez kolejne neurony trwa do chwili, gdy ostatni z nich prześle bodziec do mózgu. Wtedy czujemy ukłucie.

Sposób działania ludzkich komórek nerwowych stał się inspiracją dla osób rozwijających sztuczną inteligencję.
Pisaliśmy już o dostarczaniu maszynie danych. Oczywiście można te dane wgrywać z dysku przenośnego, maszyna może też sama pobierać je z internetu. I można podłączyć do maszyny odpowiednią bazę danych. Jednak współcześnie sztuczną inteligencję buduje się tak, by potrzebne dane dostarczała sobie sama. Do tego służą jej neurony. Oczywiście nie są to takie same neurony, jak u człowieka, ale neurony sztuczne, zbudowane na wzór ludzkiego. Zanim wyjaśnimy ich działanie, przypomnimy sobie, jak działa neuron człowieka.
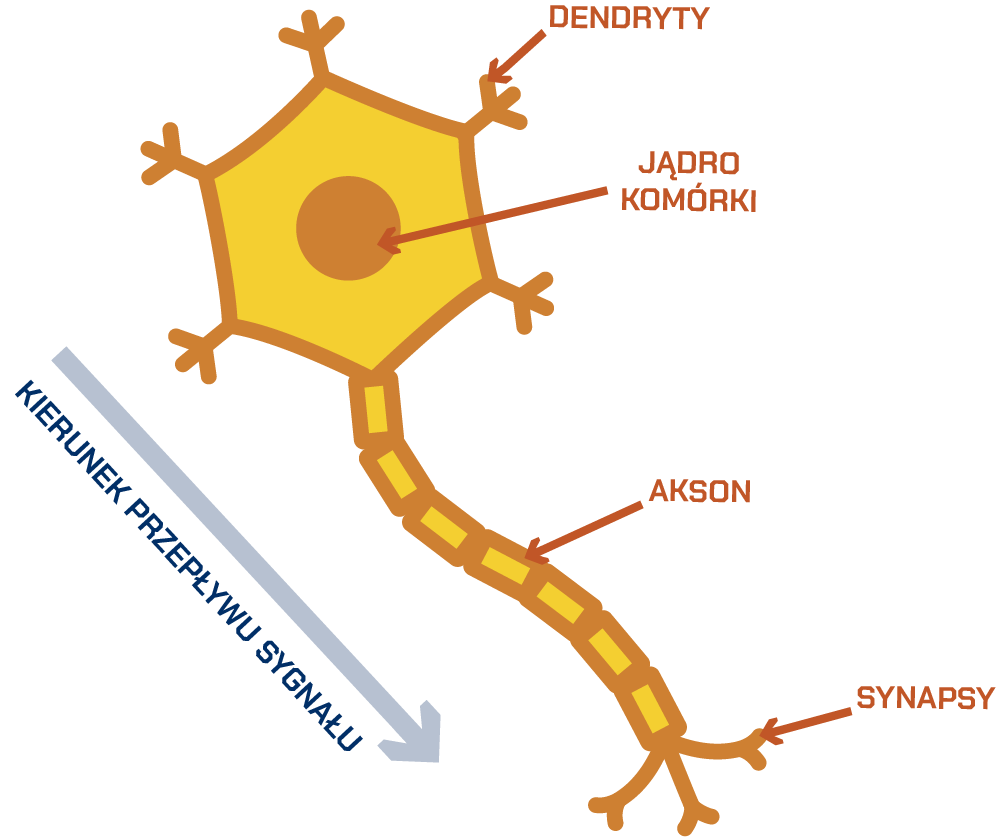
Neuron składa się z:
- dendrytów, które otrzymują od receptorów sygnały ze środowiska;
- jądra komórki,które przechowuje i powiela informację genetyczną;
- aksonu, który jest po prostu przewodem i przekazuje sygnał wejściowy dalej;
- synaps, które są połączeniem neuronu z innym neuronem, gruczołem albo mięśniem. Przekazują sygnał wyjściowy, np. uczucie bólu albo przypływ adrenaliny.
Jeden neuron w ludzkim ciele właściwie nic nie znaczy i może niewiele. Jednak w towarzystwie innych neuronów, a nawet całej ich sieci, stanowi jeden z podstawowych układów, którego człowiek potrzebuje do poznawania świata i uczenia się.
Na co dzień bombardują nas tysiące bodźców. Część z nich jest dla nas ważna, ale bardzo wiele z nich ignorujemy. Wyboru tych ważnych bodźców dokonują synapsy. To one decydują, jak silny będzie przekaz bodźca. Dlatego na wiele otaczających nas lub znanych nam rzeczy po prostu nie reagujemy.
Sztuczny neuron
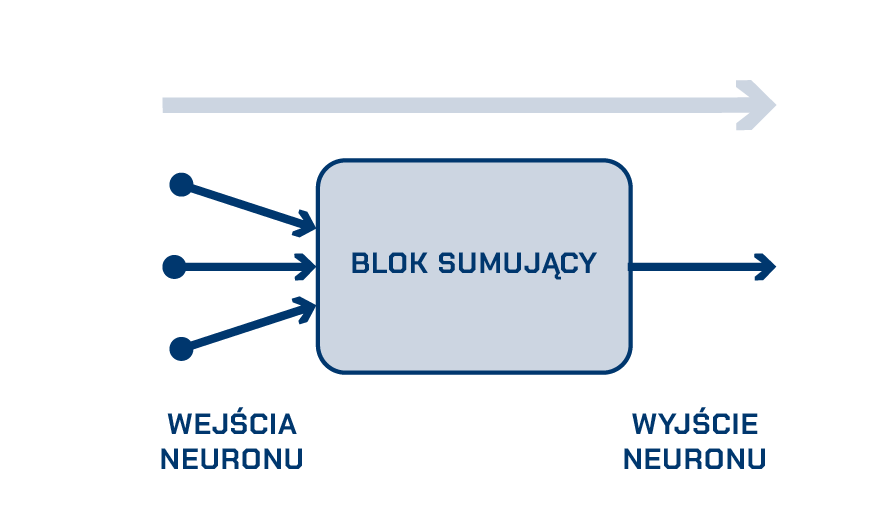
Skoro już pamiętamy, jak działa neuron biologiczny, przejdźmy do poznania neuronu sztucznej inteligencji:
- wejścia neuronu pełnią taką samą funkcję jak dendryty – czyli przesyłają sygnał;
- blok sumujący to odpowiednik jądra komórkowego w neuronie biologicznym. Przechowuje wagi. W dalszej części wyjaśnimy, czym są wagi;
- wyjście neuronu to odpowiednik synapsy. W sztucznym neuronie jest zawsze tylko jedno wyjście.
Sztuczny neuron ma mniejsze możliwości niż biologiczny. Jednak podobnie jak w przypadku neuronu biologicznego wraz z innymi sztucznymi neuronami tworzy sztuczną sieć neuronową – potężne narzędzie do nauki dla sztucznej inteligencji.
Skoro mówimy o uczeniu się sztucznej inteligencji, musimy wspomnieć o ważnym terminie z tej dziedziny, jakim jest deep learning, czyli uczenie głębokie.
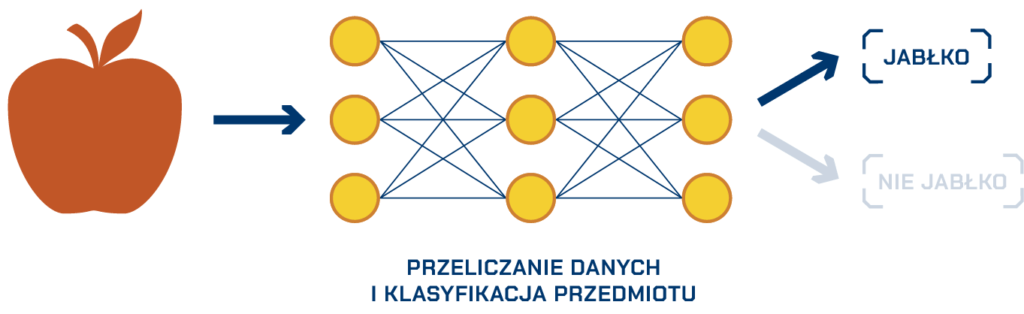
Uczenie głębokie to jedna z technik uczenia maszynowego. Niektóre sieci głębokie potrafią się uczyć bez etykiet i nadzoru człowieka. Sztuczne neurony ułożone są w kilka warstw. Warstwa zewnętrzna odbiera bodźce i przekazuje je kolejnej warstwie. Podobnie jak u człowieka, po przejściu informacji przez kilka warstw, trafia ona do „mózgu” maszyny. W naszym mózgu pojawia się informacja: „boli”, „ciepło” czy „znajoma twarz”. Do „mózgu” maszyny trafia natomiast liczba. W zależności od jej wartości, maszyna odpowiednio działa, np. rozpoznaje przedmiot albo wykonuje konkretne działanie.
Jak działa sztuczny neuron?
Mówiąc najkrócej, zbiera sygnały wejściowe, przelicza je i wysyła sygnał wyjściowy. Jego działanie wyjaśnimy na naszym ulubionym przykładzie zakupów internetowych.
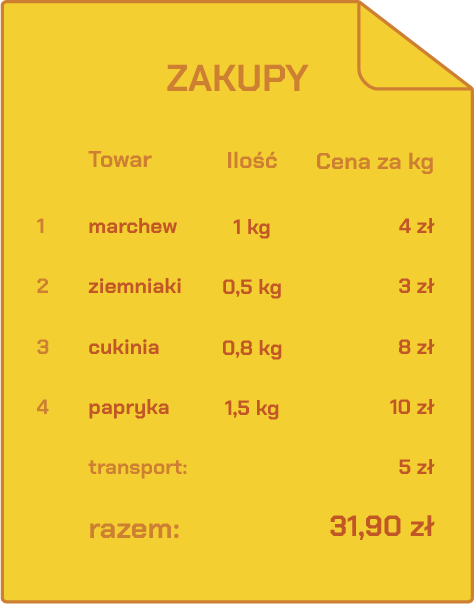
Załóżmy, że robimy zakupy w markecie spożywczym. Kupujemy różne warzywa na wagę. Jakie to warzywa, ile ich kupiliśmy i ile kosztował kilogram widzisz na poniższej liście zakupów:
Teraz przełóżmy nasze zakupy na sztuczny neuron.
Wejścia:
Ponieważ kupujemy cztery różne rodzaje warzyw, nasz neuron musi mieć cztery wejścia. Daną wejściową będzie cena kilograma każdego z warzyw, czyli:
- wejście 1: cena marchwi (4 zł),
- wejście 2: cena ziemniaków (3 zł),
- wejście 3: cena cukinii (8 zł),
- wejście 4: cena papryki (10 zł).
Wagi:
Zauważ, że każde warzywo ma inną wagę, więc nazwiemy wagi analogicznie:
- waga 1: waga marchwi (1 kg),
- waga 2: waga ziemniaków (0,5 kg),
- waga 3: waga cukinii (0,8 kg),
- waga 4: waga papryki (1,5 kg).
Żeby wszystko było jasne i proste do przeliczenia, zebraliśmy te dane w tabelce:
| towar |
wejście (cena w zł) | waga (waga w kg) | |
|---|---|---|---|
| 1 | marchew | 4 | 1 |
| 2 | ziemniaki | 3 | 0,5 |
| 3 | cukinia | 8 | 0,8 |
| 4 | papryka | 10 | 1,5 |
Stała:
To coś, co jest niezmienne, bez względu na to, ile warzyw kupimy. Będzie to opłata za transport w wysokości 5 zł.
Blok sumujący
Skoro już rozpisaliśmy sobie wagi, wejścia i stałą, to umieścimy te dane w sztucznym neuronie:
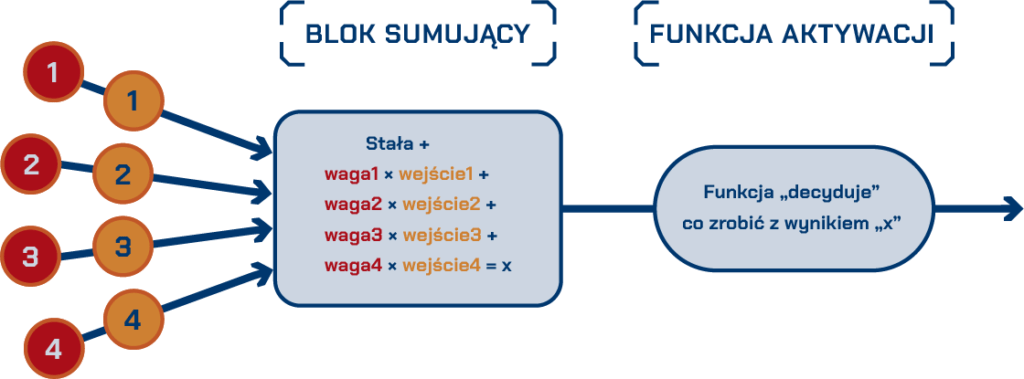
czerwone kółka – wejścia neuronu;
beżowe kółka– wagi;
blok sumujący, który wykonuje odpowiednie obliczenia na podstawie wartości wejść i wag;
blok funkcji aktywacji, który „decyduje”, co zrobić z wynikiem. Może to być prosta decyzja typu: „jeśli wynik jest większy niż 0, uruchom; jeśli mniejszy niż 0, zatrzymaj”
To teraz nieco matematyki. Wiesz, że neuron liczy wartości (wejścia, wagi i stałą) i przesyła wynik do funkcji aktywacji. Policzmy więc to, co liczyłby blok sumujący neuronu:
stała + waga1 × wejście 1 + waga2 × wejście2 + waga3 × wejście 3 + waga4 × wejście4 = ?
Podstawmy odpowiednie dane z tabeli:
5 + 1 × 4 + 0,5 × 3 + 0,8 × 8 + 1,5 × 10 = 5 + 4 + 1,5 + 6,4 + 15 = 31,9
Zatem nasz x z bloku sumującego = 31,9.
Ta liczba wysyłana jest do funkcji aktywacji. Zanim jednak do niej przejdziemy, zatrzymamy się jeszcze na chwilę przy bloku sumującym.
Do obliczeń dostaliśmy konkretne dane: wagi i wejścia. A co by się stało, gdybyśmy kupili więcej albo mniej warzyw? Oczywiście przełożyłoby się to na wynik końcowy. Jeśli każdego warzywa kupimy dokładnie o połowę mniej, to wynik, który uzyska blok sumujący, będzie wynosił 18,45, a jeśli dwa razy więcej, to wyniesie on 58,8. Zwróć uwagę, że wartości wejść pozostają w tym przypadku bez zmian, a wagi zwiększają się lub zmniejszają.
Wagi są bardzo ważne w sztucznych neuronach, bo wpływają na to, czy dany sygnał wejściowy jest ważny, czy nie. Uczenie się sztucznej inteligencji polega właśnie na ustaleniu prawidłowych wartości wag. Gdy sieć np. poprawnie rozpoznaje dany znak (np. cyfry pisma odręcznego), oznacza to, że wagi w sztucznych neuronach mają odpowiednie wartości.
Co się dzieje dalej?
Funkcja aktywacji
Blok sumujący przesyła wynik obliczeń do bloku funkcji aktywacji. Wcześniej napisaliśmy, że funkcja „decyduje”, co zrobić z wynikiem, i teraz to twierdzenie rozwiniemy.
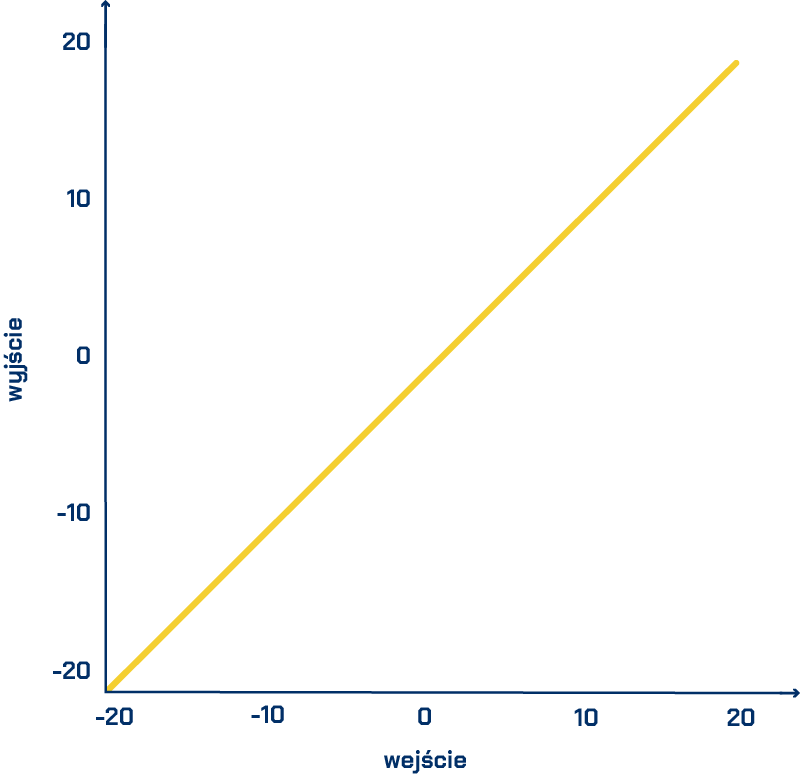
Jeśli nie pamiętasz funkcji, to nic nie szkodzi. Poniżej są wykresy trzech funkcji, które mogą być w bloku funkcji aktywacji:
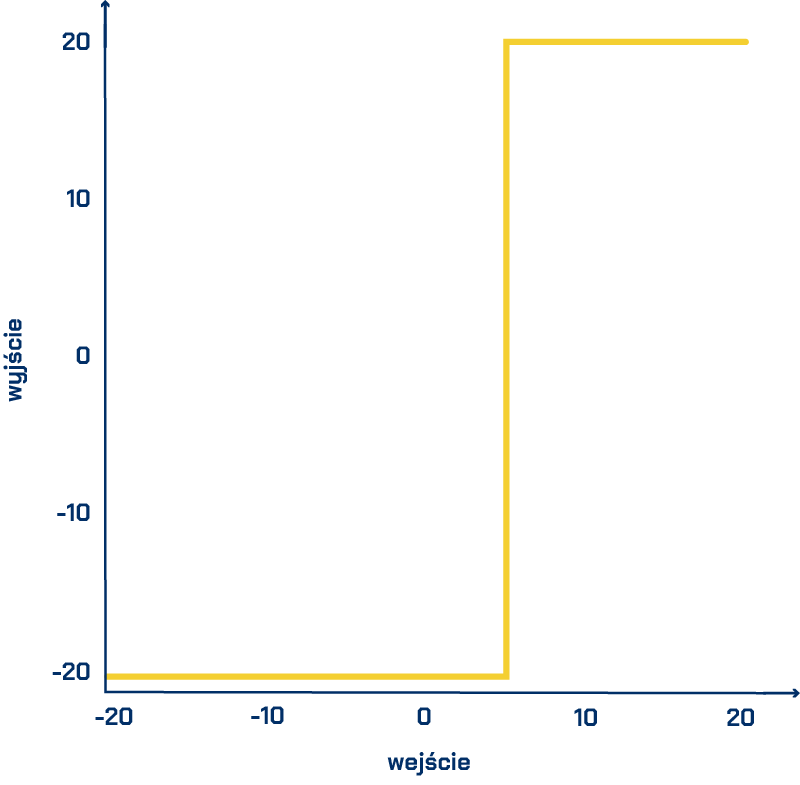
Skoro już wiesz, jak działa funkcja progowa, umieść na niej wartość 4. Jak myślisz, co się stanie?
A co się stanie, jeśli umieścisz na niej wartość -10? Czy sygnał zostanie wysłany?
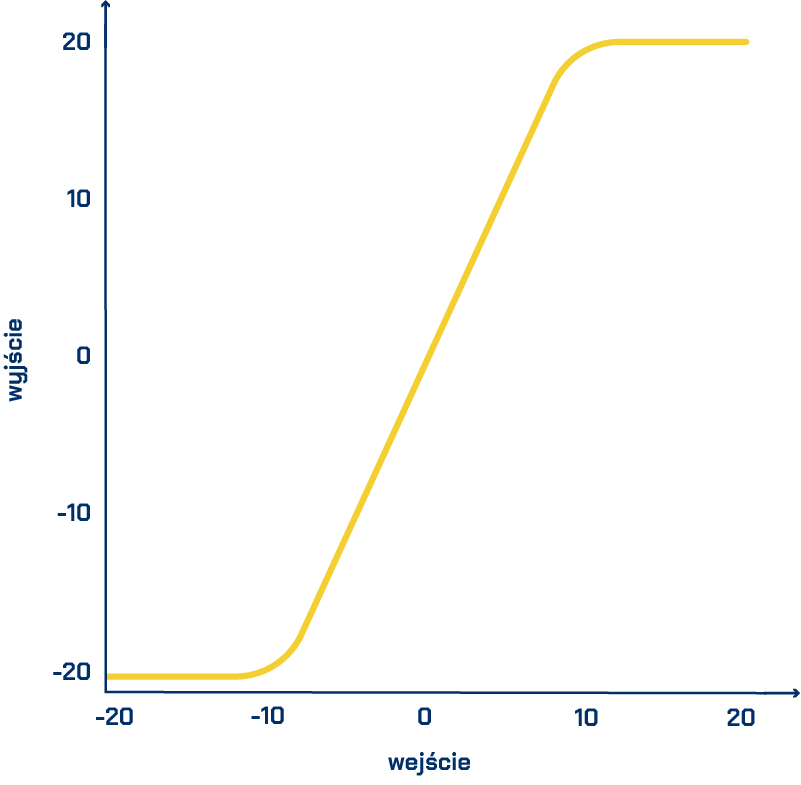
Blok funkcji aktywacji umieszcza wynik otrzymany z bloku sumującego na funkcji. Dzięki temu blok funkcji „wie”, czy ma przesłać sygnał dalej, czy nic nie robić. Oto całe działanie sztucznego neuronu!
Pamiętaj, że tak naprawdę neuron bądź jego elementy nic nie wiedzą ani o niczym nie decydują. Użyliśmy tych porównań, żeby wyjaśnić, jak to działa. W sztucznych neuronach, jak i w całej sztucznej inteligencji, wszystko polega na obliczaniu.
„Układ nerwowy” sztucznej inteligencji: sztuczne sieci neuronowe
Sieć neuronowa to wiele połączonych ze sobą sztucznych neuronów. Wyjście pierwszego neuronu przekazuje sygnał do wejścia następnego, ten przetwarza sygnał i wysyła go następnemu – i tak dalej…
Neurony w sieciach neuronowych ułożone są w warstwy. Warstw może być od kilku do kilkunastu.
Warstwa zewnętrzna (wejściowa) to ta, która rejestruje bodźce z zewnątrz. Zebrane informacje przetwarza w bloku sumującym i bloku funkcji aktywacji, a potem przekazuje (lub nie) informację następnej warstwie neuronów. Te następne warstwy nazywa się warstwami ukrytymi.
Przeliczają one informacje uzyskane od poprzedniej warstwy i przekazują następnym warstwom ukrytym lub warstwie wyjściowej.
Warstwa wyjściowa dokonuje ostatnich obliczeń tego, co otrzymały i przeliczyły wszystkie poprzednie warstwy, a następnie wysyła wynik w formie decyzji. Decyzją może być rozpoznanie jakiegoś przedmiotu, np.:
„Czy na zdjęciu jest koło?” decyzja: TAK.
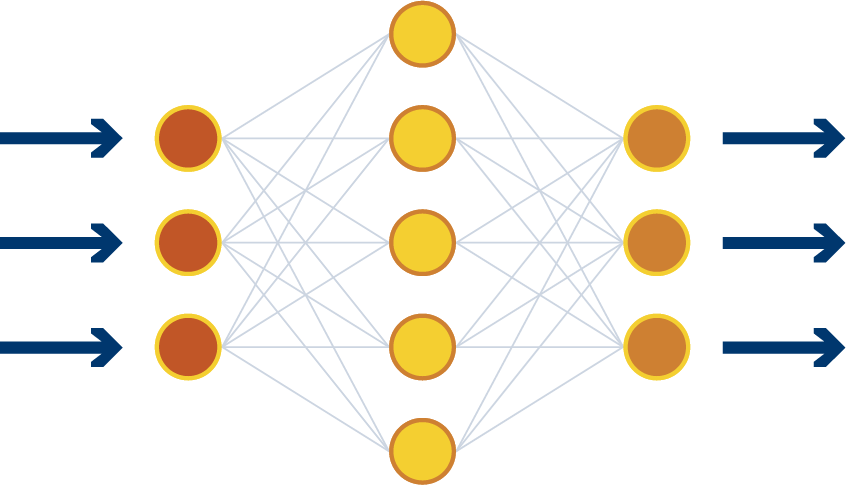
Sztucznych sieci neuronowych używa się np. do podejmowania decyzji. Dają sztucznej inteligencji ogromne możliwości. Pozwalają jej się uczyć, ale też robić niesamowite rzeczy. Na sztucznych sieciach neuronowych oparte są samochody autonomiczne, programy do rozpoznawania pisma odręcznego czy roboty humanoidalne.
Ustalanie wag, czyli „wrażliwość” sztucznego neuronu
Wagi wyjaśnialiśmy na przykładzie zakupu warzyw. Mogliśmy tych warzyw wziąć więcej lub mniej. W tym przykładzie chcieliśmy pokazać, że końcowy wynik może być różny, a wszystko zależy właśnie od wagi. Oczywiście w sztucznych neuronach nie chodzi o wagę w rozumieniu: ile coś waży, tylko o to, czy jest lub nie jest dla nas ważne. Spróbujemy wyjaśnić to na prostym przykładzie:
Jak nauczyć sztuczną inteligencję odróżniać na obrazie koło od kwadratu?
Jeśli czytałeś poprzedni artykuł, to wiesz, że SI, kiedy patrzy na obraz, by się nauczyć, co na nim widzi, analizuje każdy jego najmniejszy fragment. Taki najmniejszy fragment to piksel. Tak więc pokażemy naszej sztucznej inteligencji obraz koła. Z racji tego, że bada ona każdy piksel, rozrysowaliśmy to koło właśnie w postaci pikseli:

Wejścia: Aby sztuczna inteligencja mogła „zobaczyć” obraz i nauczyć się, że jest na nim koło, neuron, który będzie badał obraz, ma 36 wejść. Jedno wejście = zbadanie jednego piksela. Każdy piksel ma wartość 1.
Wagi: Wiesz już, że sygnał odebrany przez wejście trafia do wagi, czyli zostanie przez nią pomnożony.
Dlatego ustalimy dwie wagi:
jasny piksel = 0
żółty piksel = 1
Teraz nałożymy wagi na wejścia:
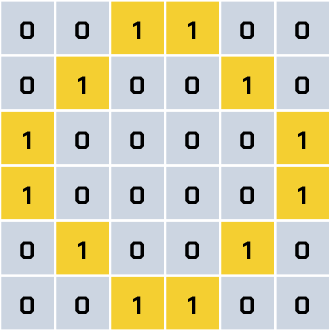
Wiemy, że w bloku sumującym neuronu wykonywane są obliczenia według wzoru:
ewentualna stała + waga1 × wejście1 + waga2 × wejście2 +… = wynik (gdzie w miejsce … wstawiamy iloczyny kolejnych wag i wejść).
Moglibyśmy rozpisać to bardzo szczegółowo rzędami, np. pierwszy rząd:
0 × 1 + 0 × 1 + 1 × 1 + 1 × 1 + 0 × 1 + 0 × 1 = 0 + 0 + 1 + 1 + 0 + 0 = 2
Jednak to nie ma sensu i byłoby czasochłonne. Możemy obliczyć to szybciej. Skoro wiemy, że mamy na obrazie 12 wag o wartości 1, to 12 × 1 = 12. Wszystkie piksele bez koloru dają wartość 0 (24 × 0 = 0), zatem neuron zwróci nam wartość 12. Czy w ten sposób sztuczna inteligencja rozpozna koło? Jeszcze nie odpowiemy na to pytanie, ale pójdziemy o krok dalej…
Teraz pokażemy sztucznej inteligencji obraz kwadratu. Wagi już nałożyliśmy na wejścia, zgodnie z tą samą zasadą, którą zastosowaliśmy przy obrazie koła.
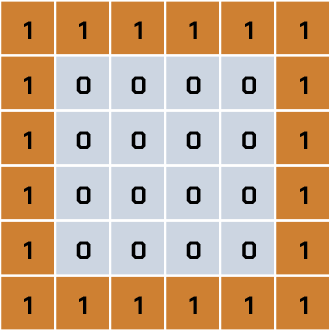
Neuron w przypadku kwadratu zwróci nam wartość 20, bo mamy 20 wag o wartości 1, a pozostałe mają wartość 0. Możesz to policzyć i sprawdzić, jeśli masz ochotę.
Teraz porównajmy nasze koło i kwadrat w liczbach.
Koło = 12, kwadrat = 20. Jak te figury na podstawie liczb rozróżni sztuczna inteligencja? Otóż… nie odróżni. W odróżnieniu koła od kwadratu pomoże sztucznej inteligencji funkcja progowa, która działa na zasadzie warunku: jeśli wynik jest większy od 0, to na obrazie jest kółko; jeśli jest mniejszy od 0, to na obrazie jest kwadrat.
Zatem w przypadku kwadratu musimy ustawić inne wagi, np. -1. Jeśli to zrobimy, to teoretycznie wynik zwrócony przez sztuczny neuron powinien wynieść -20. Wtedy funkcja progowa zadziałałaby zgodnie z warunkiem. Dość dużo tych obliczeń, prawda? A co by było, gdyby obraz miał 1000 na 1000 pikseli? Spróbujemy uprościć sprawę wag. Nałożymy więc na siebie obrazy koła i kwadratu:
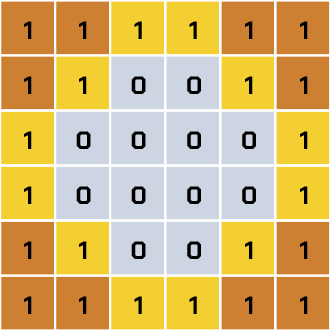
Zastanawiasz się, w czym problem? To spójrz na następny obraz, na którym piksele wspólne dla koła i dla kwadratu zaznaczyliśmy na ciemnobrązowo:
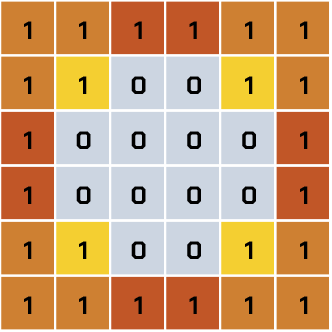
Problem tkwi w ciemnobrązowych pikselach. Skoro są takie same dla koła i kwadratu, to przyznasz, że szanse na to, by na ich podstawie sztuczna inteligencja rozróżniała te dwie figury, są znikome. Nasuwa się więc wniosek, że nie ma potrzeby ustalania dla nich wag. Pojawia się też pytanie: dla których wejść warto wagi ustalać?
Odpowiedź: dla warstw charakterystycznych dla danej figury. Warstwy charakterystyczne to takie, które pojawią się właśnie przy konkretnej figurze, a dla innej pozostają puste. Zwróć uwagę, że koło nigdy nie zapełni rogów obrazu, a kwadrat – na pewno.
Popatrzmy więc jeszcze raz na obie figury i zastanówmy się, gdzie warto ustawić wagi:

Oto proponowane rozwiązanie:
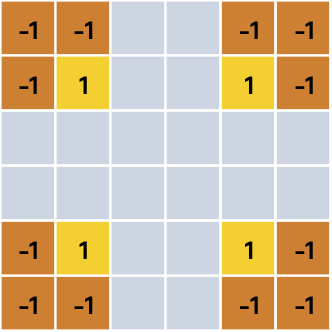
Czy jest jeszcze prostsze rozwiązanie? Oczywiście. Nie musimy ustalać wag dla każdego rogu obrazka. Moglibyśmy dla jednego w ten właśnie sposób:
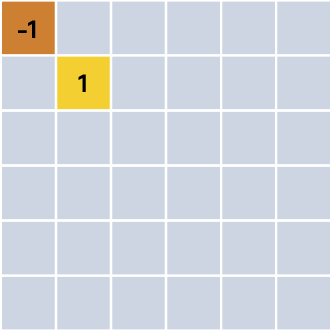
Gdy SI „zobaczy” kwadrat, wynik z bloku sumującego będzie równy -1, a gdy koło, wynik wyniesie 1. Wynik zostanie przesłany do bloku funkcji. W takich sytuacjach funkcja progowa „wybiera” zgodnie z warunkiem: Jeśli wynik jest mniejszy od 0, na obrazie jest kwadrat. Jeśli jest większy od 0, na obrazie jest koło. Wszystko się zgadza.
Pamiętaj, że omówiony przykład rozróżniania koła i kwadratu sprawdzi się tylko wtedy, gdy pokazujemy sztucznej inteligencji te dwa obrazy i zawsze są one takich samych rozmiarów. Jeśli zastanawiasz się, dlaczego, to podpowie Ci poniższy obrazek:
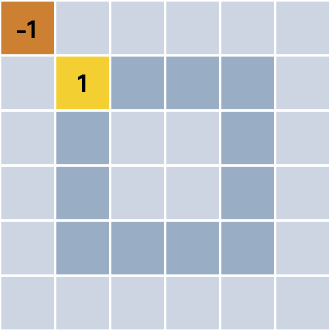
To były bardzo proste przykłady ustalania wag.
Zadanie oczywiście jest o wiele trudniejsze, gdy mamy do czynienia z figurami różnej wielkości na tym samym obrazie. Jeszcze większe trudności sprawia sztucznej inteligencji obejrzenie obrazu, który ma ogromny rozmiar. Obraz wielkości 1000 na 1000 pikseli wymagałby od neuronu… miliona wejść, żeby zbadać, piksel po pikselu, co na nim jest. W takich sytuacjach stosuje się tzw. splotowe sieci neuronowe (inaczej: konwolucyjne). Neurony w warstwie wejściowej mają o wiele mniej wejść i oglądają obraz kawałek po kawałku. Wykrywają jasne i ciemne plamki oraz konkretne kolory. Rozpoznają krawędzie i kształty elementów, a nawet ich orientację, czyli to, że np. są obrócone o 90 stopni w prawo. Najważniejszą cechą sieci konwolucyjnych jest to, że potrafią rozpoznać wspomniane kółko czy kwadrat bez względu na to, czy będzie on zajmował cały obraz, czy jego ćwierć. Rozpoznają je nawet wtedy, gdy są przechylone, w innych pozycjach niż te, w których neurony „widziały” je podczas nauki.
Czas na sprawdzenie wiedzy. Pamiętaj, że możesz zawsze sprawdzić, czy dobrze odpowiedziałeś na poniższe pytania, stosując obliczenia: waga1 × wejście1 + waga2 × wejście2… = wynik.
Wynik powinien być mniejszy lub większy od zera, gdyż w poniższych zadaniach zastosowaliśmy funkcję progową.