Z poprzedniego artykułu wiemy, że sztuczna inteligencja towarzyszy nam w codziennym życiu. Dziś niemal każdy używa map albo gier, które ją wykorzystują.

W tym artykule spróbujemy odpowiedzieć na pytania: Co to jest problem?; Jak SI rozwiązuje problemy?

Ogólnie mówiąc, to trudna sytuacja, dla której musimy znaleźć rozwiązanie. Czasami rozwiązanie jest jedno, ale może być ich wiele. Ze wszystkich możliwych rozwiązań wybierzemy najlepsze. Co znaczy „najlepsze”? To zależy od tego, co jest dla nas ważne i z czego możemy rezygnować. Najlepsze może znaczyć najszybsze, gdy zależy nam na czasie, albo najtańsze, jeśli nie chcemy ponosić dużych kosztów.

Oczywiście problem problemowi nierówny, na przykład za problem możemy uznać to, że nie mamy miliona złotych. Naszym celem będzie wtedy zdobycie takiej kwoty. Rozwiązanie może nie być proste, może wymagać systematycznego działania i czasu. Dziś sztuczna inteligencja sobie z nim nie poradzi, ale na szczęście szybko i skutecznie rozwiązuje inne problemy.

Wyobraźmy sobie, że jesteśmy w Rzeszowie na dworcu PKP. Nigdy nie byliśmy w tym mieście i go nie znamy. Nie wiemy też, jak się po Rzeszowie poruszać, a musimy dojechać komunikacją miejską na ulicę Słowackiego 11. Co robimy?

Zapewne to, co zdecydowana większość ludzi: wyciągamy smartfon i włączamy aplikację do wyznaczania trasy.

W wybranej aplikacji wpisujemy, skąd jedziemy (dworzec PKP) i dokąd chcemy dojechać (Słowackiego 11). Aplikacja poszuka możliwych rozwiązań tego problemu, czyli sposobów dotarcia z punktu A do B. Jako możliwe rozwiązania zobaczymy numer autobusu, w który musimy wsiąść, by dojechać do celu. Dodatkowo możemy widzieć czas odjazdu i podróży, a może nawet koszty podróży, czyli ceny biletów. Pozostaje wybrać rozwiązanie, z którego chcemy skorzystać.

Oczywiście z miejsca A do miejsca B może prowadzić tylko jedna linia autobusowa, ale można też dojechać tam z przesiadkami. Czy droga z przesiadkami oznacza, że jedzie się dłużej? Niekoniecznie. Czasem podróż z przesiadką może odbyć się szybciej, ale drożej, bo np. trzeba dwa razy skasować bilet. Aplikacja może (choć nie musi) uwzględniać korki, roboty drogowe, zmiany w ruchu i wyliczać nam rzeczywisty czas dojazdu na miejsce.

Aplikacje do planowania trasy rozwiązują problemy związane z wyszukiwaniem i planowaniem. Stosowane w nich algorytmy sprawdzają się nie tylko w nawigacji, ale też w grach. Nie będziemy o nich opowiadać w tym kursie. Zamiast tego przedstawimy pierwszy etap rozwiązywania problemów, czyli:

• określenie celu działania, czyli sytuacji, w której uznamy, że problem jest rozwiązany;
• znalezienie możliwych rozwiązań i wybranie najlepszego.

Zagadka I: lis, zając i marchew

Być może znasz starą zagadkę z dzieciństwa o pasterzu, lisie i zającu. Na lewym brzegu rzeki znajdują się:

• pasterz 
• lis 
• zając 
• marchewka 

Pasterz ma łódź, którą tylko on może sterować. Twoim zadaniem jest przeprawienie pasterza, zwierząt i marchwi na prawy brzeg rzeki, ale musisz przestrzegać zasad:

• obok pasterza w łódce jest miejsce na tylko jeden ładunek: zająca, lisa albo marchew
• zając nie może być sam na brzegu z lisem, bo lis go zje
• zając nie może być sam na brzegu z marchewką, bo ją zje
• tylko pasterz może powstrzymać zwierzęta od jedzenia
• pasterz, lis, zając i marchew mogą zmieniać brzeg dowolną ilość razy.

W jaki sposób pasterz może przewieźć bezpiecznie wszystkie ładunki na prawy brzeg?

Zapewne potrafisz znaleźć rozwiązanie zagadki i sztuczna inteligencja nie jest Ci do tego potrzebna. W tym rozdziale chcemy jednak pokazać, jak problemy rozwiązuje właśnie sztuczna inteligencja.

Stany elementów

Zaczniemy od rozpisania stanów każdego z ruchomych elementów tej zagadki: pasterza, lisa, zająca i marchewki. Łódź służy tylko do transportu i zawsze jest tam, gdzie pasterz, dlatego nie będziemy uwzględniać jej stanu.

Stan elementu to jego położenie względem rzeki. W naszej zagadce element może być na jej prawym (P) lub lewym (L) brzegu, czyli mieć dwa stany. Możliwości ułożenia tych stanów nazywamy kombinacjami. Wszystkich kombinacji jest 16.

Teraz nie będziemy analizować kolejności przepraw na drugi brzeg. Zajmiemy się wszystkimi kombinacjami, czyli rozpiszemy, na których brzegach mogą być wszystkie elementy.

Żeby było łatwiej zrozumieć nasz zapis, wytłumaczymy go na kilku przykładach:

Pozycja 1 tabeli to start naszej gry. Wszystkie elementy są po lewej stronie brzegu, dlatego w skrócie zapisaliśmy kombinację LLLL (jedna litera to stan kolejnego elementu z tabeli). Kombinacja nr 2 LLLP oznacza, że pasterz, lis i zając są po stronie lewej, a marchew po prawej stronie rzeki, itd.

Kombinacja, do której chcemy dojść, to wszystkie elementy po prawej stronie rzeki, czyli PPPP (pozycja 16 w tabeli). W poniższej tabeli znajdują się wszystkie możliwe stany elementów. Jeśli chcesz, możesz sobie rozpisać je samodzielnie i sprawdzić.

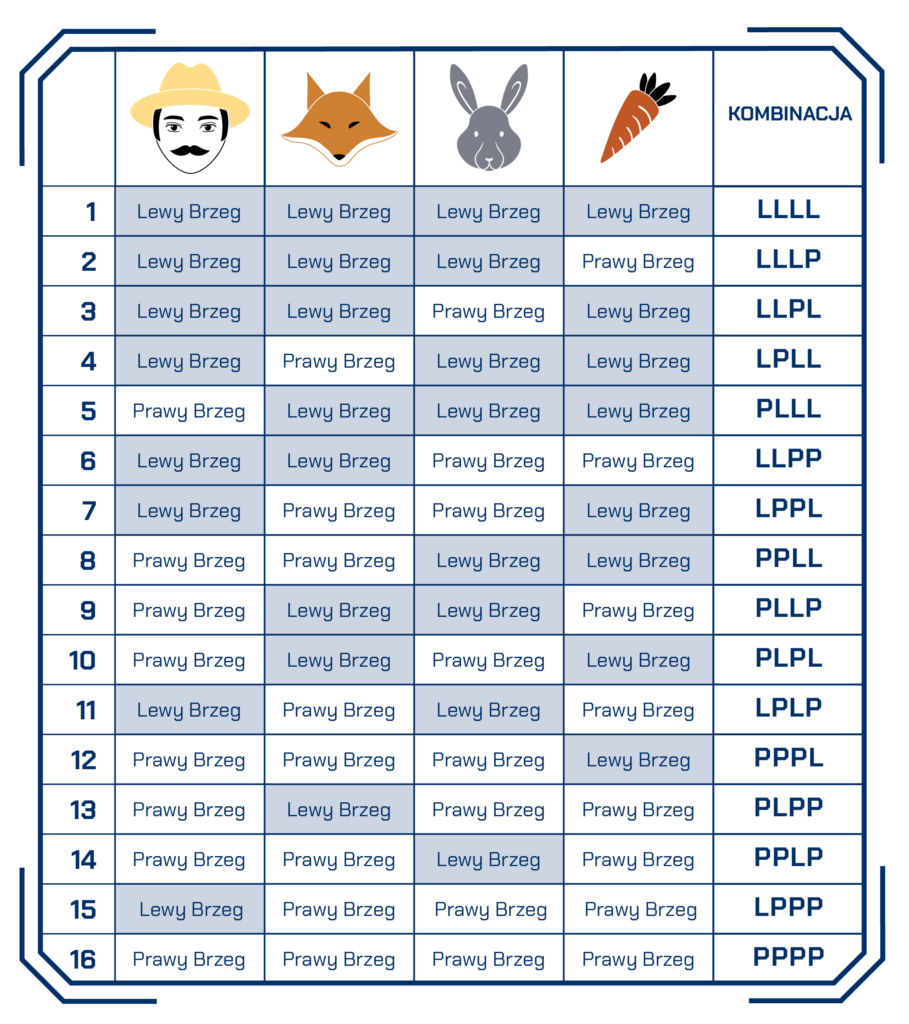
Teraz musimy na chwilę wrócić do zasad naszej zagadki. Pamiętajmy, że:

• zając nie może być sam na brzegu z lisem, bo lis go zje
• zając nie może być sam na brzegu z marchewką, bo ją zje

Oznacza to, że takie kombinacje kończą naszą grę. Musimy więc wykreślić je z tabelki. Sytuacje, w których te elementy są na innym brzegu niż pasterz to numery: 5, 6, 7, 8, 9, 15. Po usunięciu ich z tabeli zostaje nam 10 możliwych kombinacji gry, które doprowadzą nas do rozwiązania:

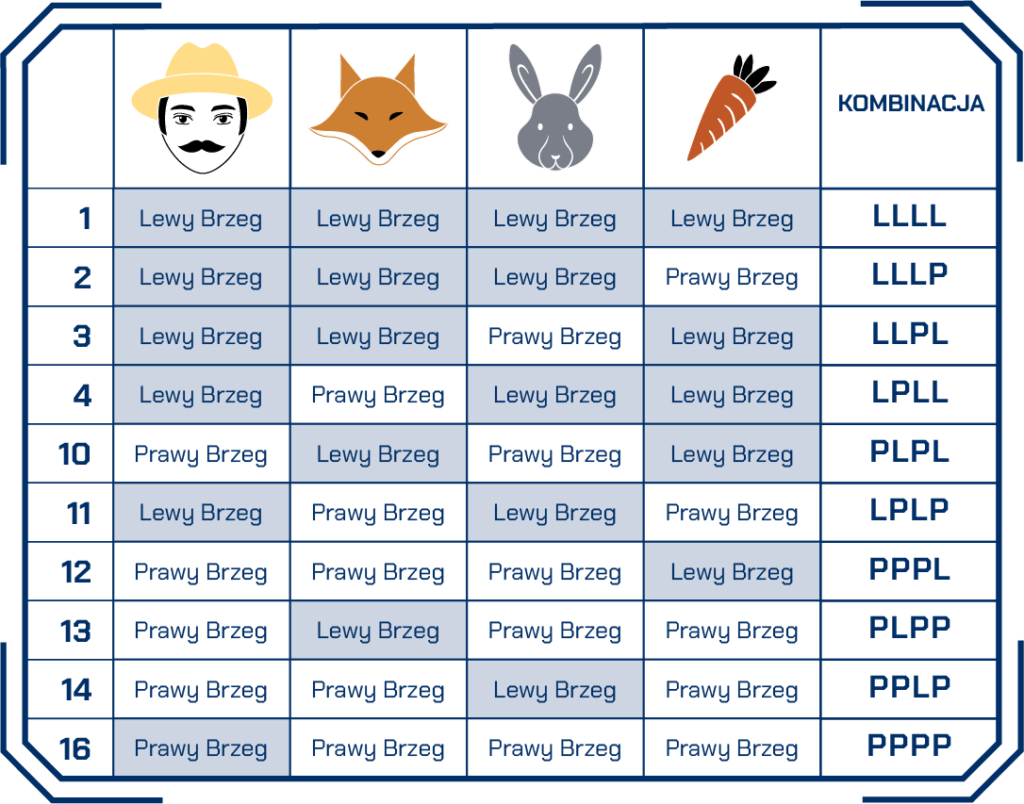
Przejścia między kombinacjami

Kolejna rzecz, którą musimy zrobić, to ustalić, które kombinacje można ze sobą połączyć. Dzięki temu dojdziemy do rozwiązania zagadki. Żeby sobie uprościć to zadanie, po lewej stronie rzeki umieścimy te, w których pasterz jest także po lewej stronie, a po prawej te, w których jest po prawej. Zrobimy tak dlatego, że to pasterz przewozi ładunki, więc za każdym razem zmienia swój stan z L na P i odwrotnie. Dzięki temu możemy płynnie przechodzić z lewej do prawej strony obrazka i znów wracać do lewej. Wygląda to tak:

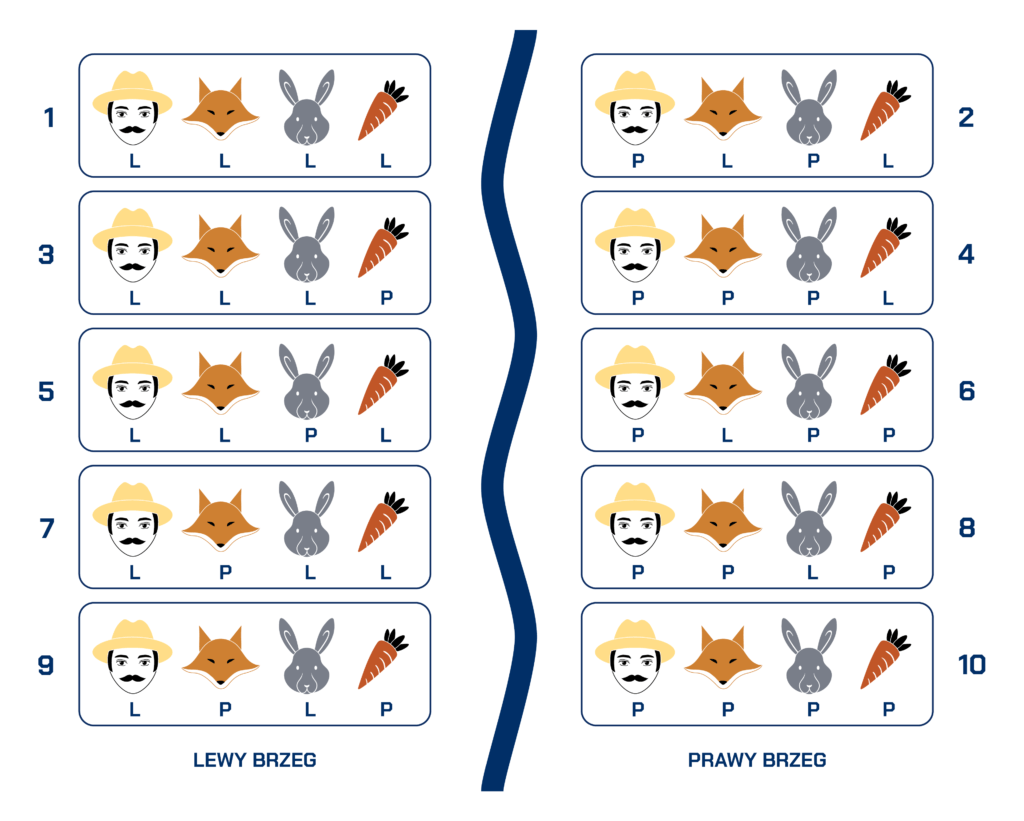
Uwaga! Numery przy kombinacjach nie są ich kolejnością. Pozwalają one jedynie odwołać się do konkretnego stanu przy tłumaczeniu tego ćwiczenia.

A teraz rozwiążemy zagadkę:

kombinacja nr 1 (start)

Wszystkie elementy są po lewej stronie. Wiemy, że pasterz może zabrać tylko jeden ładunek. Zatem musimy po prawej stronie znaleźć stan, w którym pasterz jest z innym elementem w stanie P, a reszta elementów zostaje po lewej stronie rzeki (L).

kombinacja nr 2

To stan, którego szukaliśmy: pasterz z zającem są po prawej stronie rzeki, lis i marchew zostali po stronie lewej. Teraz pasterz powinien zostawić zająca i wrócić na lewy brzeg.

kombinacja nr 5

Pasterz wrócił na lewy brzeg. Jest na nim wraz z lisem i marchewką, a zając jest po prawej. Co dalej? Pasterz może popłynąć na prawy brzeg z marchewką lub lisem. Musimy wybrać jedną z tych opcji.

kombinacja nr 4

Pasterz zabrał ze sobą lisa, więc po lewej stronie rzeki mamy marchew, a po prawej pasterza, zająca i lisa. Pamiętaj, że pasterz nie może wrócić sam. Zostawiłby lisa i zająca samych, co skończyłoby się zjedzeniem tego drugiego. Nawet nie mamy takiego stanu do wyboru, bo wykluczyliśmy go jako oznaczający „przegraną”. Pasterz musi zabrać któryś element. Ponieważ dopiero co przypłynął z lisem, zabieranie go z powrotem oznaczałoby powrót do poprzedniego stanu gry.

kombinacja nr 7

Pasterz zabrał zająca. Jest z nim i marchewką po lewej stronie. Po prawej pozostał lis. Nie ma sensu zabierać na prawą stronę zająca, bo dopiero co tam był. Zabierzmy więc marchew.

kombinacja nr 8

Pasterz, marchew i lis są po prawej stronie, po lewej został zając. Co to oznacza? Pasterz może bezpiecznie wrócić sam na lewy brzeg.

kombinacja nr 9

Pasterz z zającem są po stronie lewej, a lis i marchew po prawej. Pozostał nam ostatni ruch, który prowadzi do rozwiązania zagadki.

kombinacja 10 (meta)

Jedyny ruch, jaki nam pozostał, to przepłynięcie pasterza i zająca na prawy brzeg. Wszyscy są w komplecie!

Wszystkie nasze ruchy potrzebne do rozwiązania zagadki widać na poniższym obrazku:

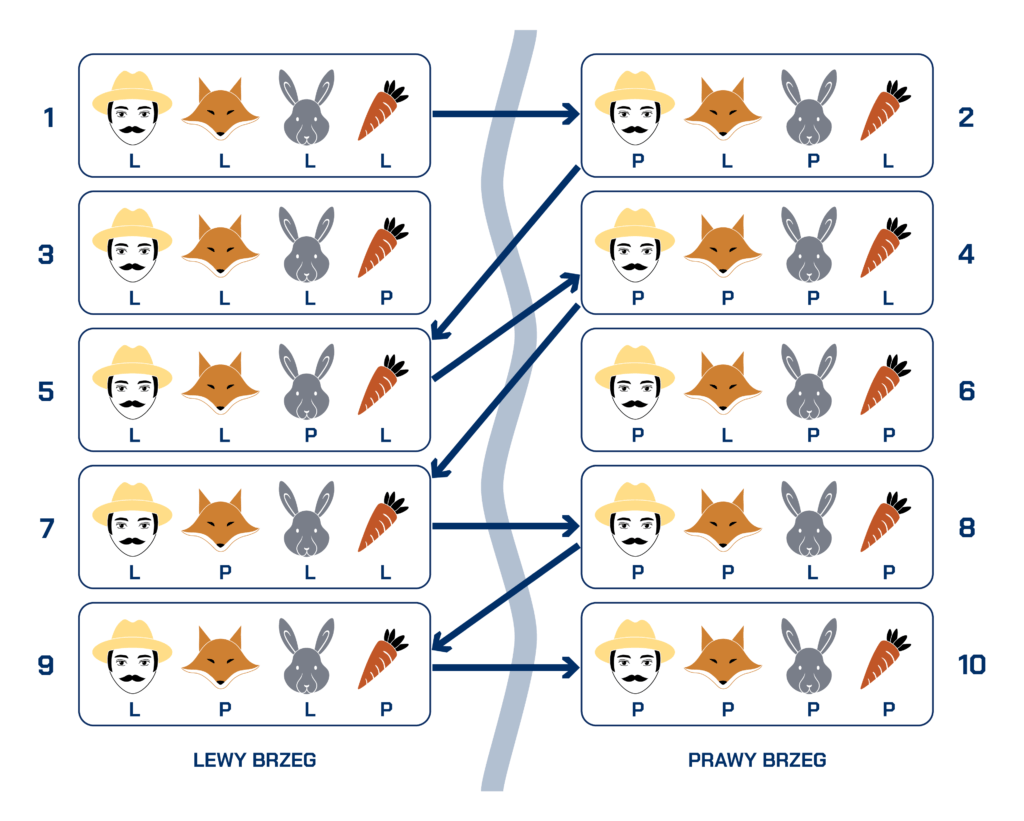
Podczas naszej gry przeszliśmy przez osiem kombinacji siedmioma ruchami. Było to jedno z dwóch rozwiązań.

Gdy rozwiązywaliśmy tę zagadkę, na każdym kroku sprawdzaliśmy, kto jest na którym brzegu, czy ruch został wykonany sensownie i co nam dał. Mimo że odrzuciliśmy stany kończące grę, to i tak sprawdzaliśmy, czy czasem lis nie zostanie sam na sam z zającem, prawda?

Sztuczna inteligencja tego nie robi. Ona przechodzi do pierwszej możliwej kombinacji. Najlepiej pokazuje to pierwszy ruch, z kombinacji nr 1 do kombinacji nr 2:

Jak o tym ruchu myśli człowiek? „Trzeba przeprawić pasterza z królikiem, bo wtedy lis i marchew zostaną na lewym brzegu i nikt nikogo nie zje”.

Jak o tym ruchu „myśli” sztuczna inteligencja? „Mogę przenieść naraz dwa ładunki, w tym zawsze pasterza. Muszę więc przejść do takiej kombinacji, w której dwa elementy są w stanie P, a reszta w stanie L. Jedyna z możliwych kombinacji to nr 2”.

Gdybyśmy umieli wytłumaczyć, jak „myśli” SI, to tak by to mniej więcej wyglądało. Sztuczna inteligencja nie sprawdza, czy lis zje zająca, bo takie stany już odrzuciliśmy. Żaden z tych stanów, które zostały, nie kończy gry. A my, ludzie, wciąż sprawdzamy konsekwencje ruchu.

Oczywiście używamy cudzysłowu, bo tak naprawdę SI nie myśli. Wykonuje pewne zadania zgodnie z instrukcją, tyle że my chcemy wytłumaczyć, jak to robi, porównując to do działania człowieka.

Przyznajmy, że „myślenie” sztucznej inteligencji jest całkiem inne od myślenia człowieka. Warto poznać kilka ważnych terminów, których użyliśmy do opisania rozwiązania zagadki:

Kombinacje

To wszystkie możliwe ustawienia elementów, czyli sytuacje, które mogą wystąpić w grze. W naszej zagadce kombinacjami były ułożenia elementów względem rzeki. Jeśli problemem jest przejazd z miejsca A do miejsca B, to kombinacjami mogą być lokalizacje A, B i np. te, obok których chcemy przejechać.

Przejścia

Przejście to bezpośrednie połączenie między kombinacjami. W zagadce przejściem był ruch z kombinacji nr 1 do kombinacji nr 2, czyli przepłynięcie pasterza i zająca na prawy brzeg. Wszystkie ruchy od startu do mety to droga.

Każdy z nas zna grę w kółko i krzyżyk. Bierze w niej udział dwóch graczy, którzy na planszy 3 na 3 pola stawiają swoje znaki, czyli O lub X. Postawienie swojego znaku w linii poziomej, pionowej lub na ukos oznacza wygraną.

Takie gry jak kółko i krzyżyk, szachy czy warcaby są problemami, z którymi sztuczna inteligencja radzi sobie o wiele lepiej i szybciej niż człowiek.

Nie będziemy tutaj wyjaśniać, jak należy grać w kółko i krzyżyk, bo przecież doskonale to wiemy. Przeanalizujemy etapy tej gry i wytłumaczymy na jej przykładzie, jak „myśli” SI.

Z poprzedniej zagadki wiemy, że aby rozwiązać problem, sztuczna inteligencja sprawdza stany elementów lub ich kombinacje, a następnie je łączy. W tej grze będzie bardzo podobnie. Aby SI mogła grać z nami w kółko i krzyżyk, należy przygotować jej tzw. drzewo gry.

Drzewo gry

To schemat przebiegu gry. W przypadku gry w kółko i krzyżyk przedstawia wszystkie kombinacje znaków O i X na planszy. Te kombinacje nazywają się węzłami. Drzewo wygląda jak diagram, na samej górze jest pusta plansza, czyli start. Pod nią są rozpisane kolejne możliwe ruchy (węzły) pierwszego gracza. Pod nimi są możliwe ruchy przeciwnika – i tak na zmianę. W efekcie węzły prowadzą do zakończeń gry. Zakończenie gry to wygrana X, wygrana O lub zapełniona plansza.

Rozrysowanie całego drzewa gry w kółko i krzyżyk byłoby bardzo czasochłonne i zbyt trudne, żeby je wytłumaczyć. Zaczęlibyśmy od pustej planszy. Potem rysowalibyśmy dziewięć wariantów postawienia kółka i dalsze możliwe ruchy. Nasze drzewo gry byłoby ogromne. Skupimy się więc na grze od pewnego momentu, gdy gracze O i X już postawili na planszy swoje znaki. Wygląda to tak:

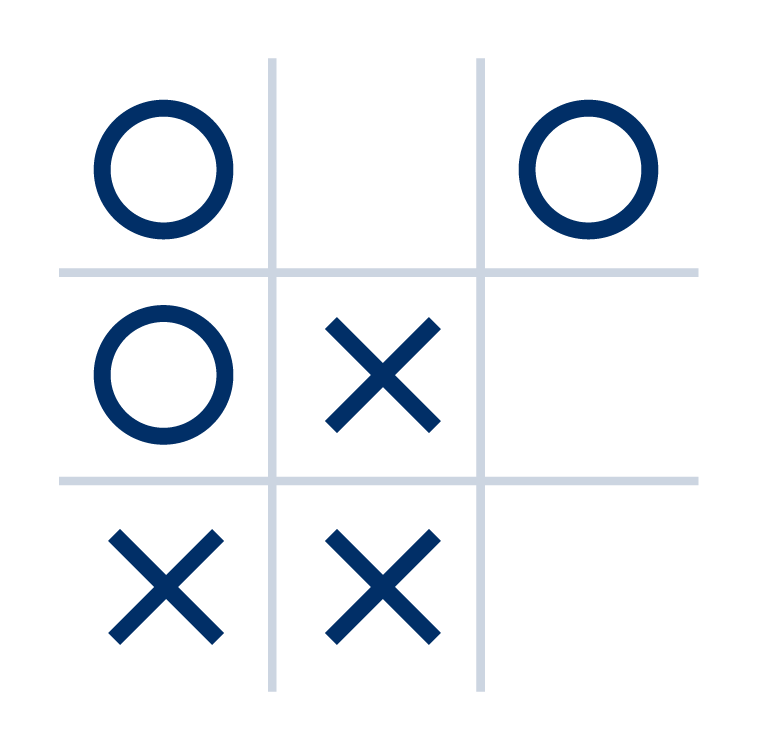
Każdy z graczy wykonał trzy ruchy. Pozostały trzy pola wolne. Ostatni postawił znak gracz O, więc musimy zapisać kolejne możliwe ruchy dla gracza X. Po nich rozpiszemy ich konsekwencje, czyli znów możliwe ruchy gracza O. Zobaczmy, jak wygląda dalej rozpisane drzewo gry:

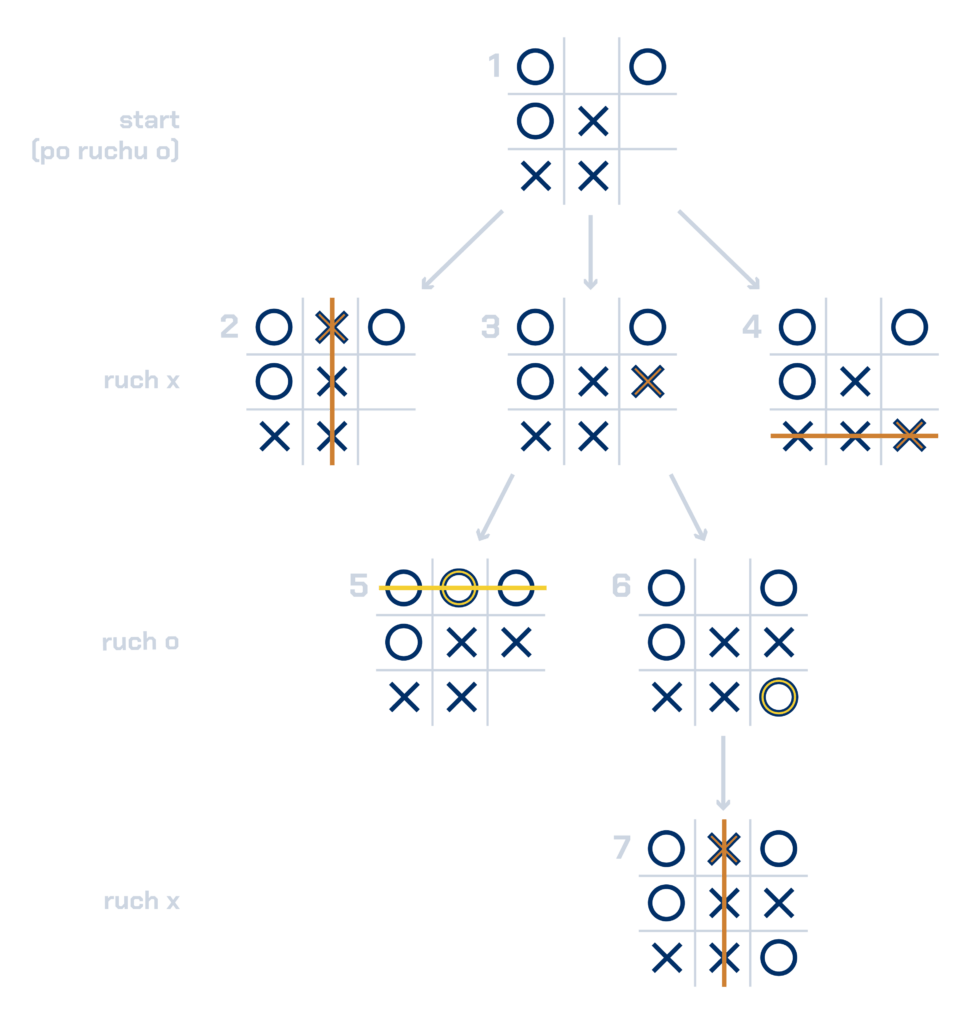
Przeanalizujmy teraz nasze drzewo gry. Po jego lewej stronie jest informacja o tym, który gracz stawia swój znak. Zwróć uwagę, że każdy węzeł (plansza gry) ma swój numer na dole.

Węzeł nr 1 przedstawia stan, jaki był na planszy, gdy gracz O postawił swój znak.

Węzły 2, 3 i 4 pokazują wszystkie możliwości postawienia znaku X (trzy, bo pozostały trzy pola do zapełnienia, a jest to ruch X). Od razu widzimy, że węzeł 2 i 4 kończą grę. Gdyby X postawił tam krzyżyk, wygrałby. Jednak jesteśmy tylko ludźmi i pewnych rzeczy czasem nie zauważamy. Dlatego musieliśmy rozrysować wszystkie dalsze możliwe ruchy.

Jeśli założymy, że gracz X postawi krzyżyk tam, gdzie pokazuje węzeł nr 3, to gracz O ma szansę na wygraną (węzeł 5). Jeśli tę szansę zaprzepaści (węzeł 6), wygrana należy do gracza X (węzeł nr 7).

Przeanalizowaliśmy zagadkę o lisie, zającu i marchewce oraz grę w kółko i krzyżyk. Zapewne zauważyliśmy, że w grze dążymy do mety przy najmniejszej liczbie ruchów. Nazywamy to optymalizacją gry.

W grze w kółko i krzyżyk gracz X mógł wygrać prawie natychmiast. Wystarczył tylko jeden ruch (węzeł nr 2) i gra byłaby zakończona. Już węzeł nr 1 wskazywał, że ten gracz ma wygraną w kieszeni. Wszystkie kolejne ruchy to konsekwencje braku optymalizacji.

Podobnie było, gdy przeprawialiśmy pasterza ze zwierzętami na drugi brzeg rzeki: pewnych ruchów nie wykonywaliśmy, bo nie było sensu. Na przykład gdy dopiero co przypłynęliśmy z zającem na prawy brzeg, w kolejnym ruchu nie było sensu wracać z nim na lewy, bo to oznaczało brak postępu w grze. Dotarcie do mety trwałoby dłużej i kosztowało nas niepotrzebne ruchy.

Dlatego sztuczna inteligencja zakłada, że każdy gracz gra tak, by jak najszybciej dotrzeć do wygranej. My, grając z kimś w kółko i krzyżyk, także staramy się jak najszybciej osiągnąć swój cel, jednocześnie próbując przeszkodzić w tym rywalowi.

Obecnie w przypadku bardzo dużych gier nie rysuje się drzewa decyzyjnego.

Dlaczego?

Wyobraźmy sobie, że ktoś musiałby rozrysować wszystkie możliwe węzły w drzewie gry w warcaby, i to zaczynając od pustej planszy! To raczej niemożliwe, a nawet gdyby było możliwe, zajęłoby mnóstwo czasu i zawierało sporo błędów. Dlatego do tworzenia takich gier stosuje się algorytmy. Sprawdzają one możliwości ruchów i wygranych oraz przegranych.

Algorytm o nazwie min-max stosowany jest w grze w kółko i krzyżyk. Przewiduje konsekwencje ruchów i wybiera najlepszy dążący do zwycięstwa. Zaledwie kilka linijek kodu programistycznego „potrafi” świetnie grać w tę grę!

Algorytm A* (czytaj: A-gwiazdka) potrafi kierować postacią w grze z punktu A do punktu B. Szuka dla niej najlepszej drogi do poruszania się, omijając przeszkody czy wrogów. Zastosowano go w popularnej grze F.E.A.R z 2005 roku. Ten sam algorytm stosuje się też do… rozpoznawania mowy.

Różnica między algorytmem a SI

W artykule mówiliśmy o algorytmach i o sztucznej inteligencji. Warto znać różnicę miedzy nimi. Już podawaliśmy definicję algorytmu i kilka nieformalnych definicji SI, bo formalnej wciąż nie ma. Teraz jest dobry moment, by wytłumaczyć to dokładniej.

Algorytm to wszystkie czynności, które po kolei trzeba wykonać, żeby osiągnąć cel. Możemy to porównać do przepisu na ciasto: wiemy, jaki składnik i kiedy dodać, kiedy wymieszać i jak długo piec, by powstało ciasto. W informatyce jest to instrukcja, często prostsza, niż się nam wydaje. Dużo algorytmów można zapisać tak: „jeśli x ∀ to y”, ale są też bardziej skomplikowane. Wszystko zależy od tego, ile kroków algorytm musi wykonać i jak trudne jest osiągnięcie celu.

Sztuczna inteligencja to zbiór wszystkich algorytmów, które mogą rozwiązywać problemy w nieprzewidzianych okolicznościach. Dla porównania, kółko i krzyżyk to jeden algorytm min-max. Komputer ma zbiór zasad i wie, jak grać, a nawet, jak grać, by wygrać. Ale autonomiczny samochód ma już wiele algorytmów, które pomogą mu dojechać do celu. Samochód autonomiczny „nie wie”, co może spotkać na drodze. Czeka go zmiana świateł, kręta droga, piesi, inne samochody itp. Droga jest nieznana, ale dzięki wielu algorytmom z sukcesem pokonywana. Jeden algorytm by sobie z tym nie poradził.